개요
gradient descent에 대해서 배운다.
내용
gradient descent는 체계적인 방법으로 최소한의 크기의 w, b 값을 찾아주는 알고리즘이다.
gradient descent는 딥러닝을 포함한 머신 러닝의 전반적인 곳에서 쓰인다.
gradient descent 의 전반적인 내용에 대해서 살펴보자.

gradient descent 는 어떠한 함수에도 적용할 수 있고 함수들은 n 개의 인자를 가진다. 우리는 최소한의 크기를 가진 cost function을 찾으려고 한다.
이를 위해 w, b 값에 대한 초기 추측값을 가지고 시작한다. linear regression의 경우 초기값이 무엇인지간에 크게 상관이 없어서 보통 w, b의 초기값을 0으로 잡고 시작한다. 우리가 할 것은 J(w) 값을 최소화하기 위해 초기값에서부터 끊임없이 w, b 값을 수정해나가는 것이다. 그렇게 해서 최소한의 값에 다다를 때 까지 반복한다. 함수의 형태는 포물선이 아닐 수도 있으며, 몇몇 함수는 최소화된 값이 1개보다 많을 수도 있다.
아래 그림을 보자

위에 나타난 그래프는 linear regression에서 봤던 cost function과 달리, 포물선 형태로 나타나는 대신 여러 곳이 울퉁불퉁하게 튀어나와 있다. 이러한 형태는 종종 신경망 모델을 학습시킬 때 나타난다.
위 그래프 표면의 높이는 cost function 값에 해당한다.
만약 여러분이 아래 그림과 같이 가장 높은 지점에서 가장 낮은 지점까지 효율적으로 내려가기 위한 방법을 강구한다고 해보자.

우리는 360도를 돌아서 어느 방향으로 발을 딛였을 때 아래 지점으로 가장 빨리 이동할 수 있을지를 체크한다.
그렇게 하여 찾은 효율적인 방향으로 한 걸음 내딛는데, 이 방향을 수학적으론 steepest descent 방향이라고 한다. 이 방향은 다른 어떤 방향과 비교했을 때 제일 빠르게 아래 지점으로 이동할 수 있는 방향이다.
위 과정을 반복하면 제일 아래 지점으로 이동할 수 있다.
gradient descent는 이처럼 위에서 아래로 내려갈 때 가장 좋은 지점이 어디인지 알려주는 역할을 한다.
만약 여러분이 초기 w, b 값을 다르게 주어 위 과정을 처음부터 반복한다고 했을 때 그림은 아래와 같다.

위 그림처럼 또 다른 아래 지점에 도착하는 것을 볼 수 있다. 이 경우 초기값은 앞선 예제보다 조금 더 오른쪽에서 시작했을 뿐인데 다른 최소 지점에 도달하게 된다. 이들은 각각 local minima (극소점, 고립된 최소값)라고 부른다. local minima라고 부른 이유는 아래지점으로 이동하는 경로를 탈때 최종적으로 다다르는 아래 지점이 다르기 때문이다. 첫번째 아래지점으로 가는 경로를 탈때 절대로 두번째 아래지점으로 이동하는 경로에 다다를 수 없다. 반대도 마찬가지.
이제 gradient descent 를 어떻게 실제로 적용하는지 살펴보자.

위 공식은 gradient descent 알고리즘에 대해 나타낸 것이고 세부 설명은 아래와 같다.
w를 w 빼기 알파 곱 d/dw 곱 J(w,b) 으로 업데이트한다는 뜻인데 이때 알파는 learning rate(학습률) 라고 부른다.
학습률은 보통 0과 1사이의 양의 소수값이며 위에서 밑으로 내려올 때의 한 걸음의 크기를 조절한다.
그래서 만약 알파값(학습률)이 크다면 위에서 밑으로 내려올 때의 한 걸음의 크기가 매우 크다고 할 수 있고 동시에 매우 공격적인 gradient descent 과정이라고도 말할 수 있다. 반대로 작다면 한 걸음의 크기가 매우 작다고 할 수 있다.
이제 보라색 직사각형으로 칠해진 표현식에 대해서 알아보자. 이는 cost function J의 Derivative term, 즉 미분이다. 이는 위에서 밑으로 내려올 때 어떤 방향으로 걸음을 내딛을 지에 대해 의미한다. 이를 알파와 엮어서 얘기한다면, 즉 알파 곱 d/dw 곱 J(w,b) 은 위에서 밑으로 내려올 때 얼마만큼 내려오고 싶은지에 대한 크기를 의미한다.
인자는 w 뿐만 아니라 b 도 있으므로 b에 대한 공식또한 따로 존재하며 공식은 w와 비슷하나 b에 대해서 미분을 한다는 것이 다르다.
앞서 3차원 그래프의 맨 윗꼭지에서 아래 지점으로 이동했던 것을 기억해보자, gradient descent 알고리즘은 위 공식 대입을 알고리즘이 수렴할 때까지 반복을 한다. 수렴한다는 것은 local mimima(minimum)에 다다라서 w, b가 더 이상 변하지 않고, 더이상 내딛을 걸음이 없다는 것을 의미한다.
gradient descent 알고리즘을 정확히 실행하는 방법에 대한 좀 더 자세한 설명에 대해 살펴보자(중요). 위에서 아래로 내려올 때마다 w, b는 동시에 수정이 되야한다.
이를 위해서 아래 그림과 같이 d/dw * J(w,b) 와 d/db * J(w,b) 를 계산하는 동시에 w, b 값을 수정한다. 한마디로 미분한 값을 계산하는 동시에 할당하는 작업이 같이 이뤄져야 한다는 말이다.
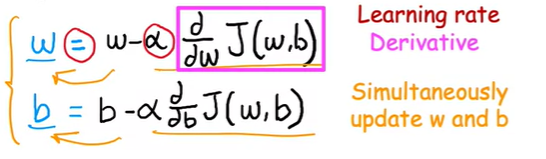
이를 코드로 표현하면 아래와 같다.

왼쪽은 동시에 수정하는 작업을 올바르게 한 것이고, 오른쪽은 올바르지 않게 한 것이다.
tmp 라는 임시변수에 공식을 적용한 값 결과를 저장한 뒤, 일괄적으로 임시변수에 있는 값을 w, b 에 다시 할당하는 것을 확인할 수 있다. 실제로도 이렇게 작업을 하는 것이 gradient descent가 자연스럽게 동작하도록 할 수 있게 하는 것으로 알려져 있다.
이제 위 공식의 learning rate와 derivative에 대한 직관적인 이해 및 두 변수를 곱하는 이유에 대한 추가 설명을 한다.
이를 위해 예제를 살펴보자, 아래 예제는 기존 J(w,b) 에서 b를 0으로 설정하여 간편화시킨 형태이며 이로 인해 w 값만 수정하게 된다, 최종적으론 w 값을 수정하면서 최소화된 크기의 J(w) 값을 얻고자 한다.
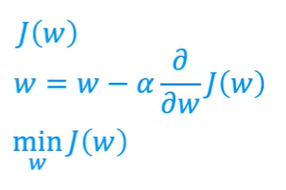
이는 아래 그래프와 같은 형태로 표현할 수 있고 해당 w값에서 gradient descent가 J(w) 함수에 대해 어떻게 동작하는지를 보자.
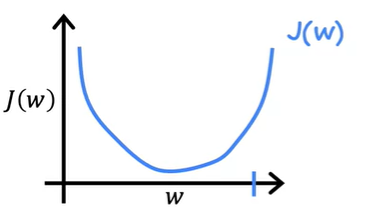
위에서 찍힌 지점의 w값에서 gradient descent는 아래 공식으로 w 를 수정시킨다. 이때 d/dw * J(w) 부분에 대해서 더 알아보자.
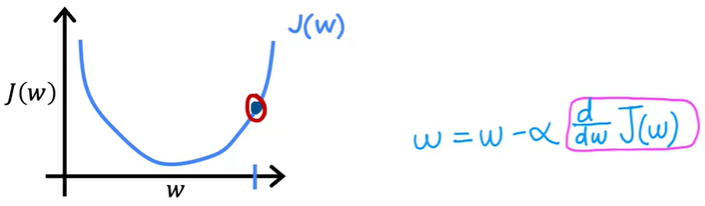
보라색 박스로 칠해진 위 부분은 해당 점에 대한 기울기, 즉 탄젠트 값이자 해당 점에서의 J함수의 미분 계수이다.
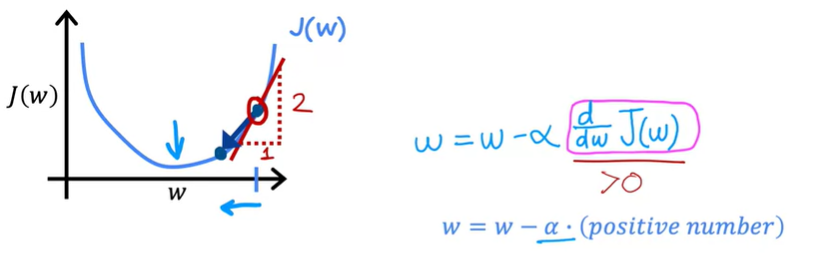
위 그림의 경우 기울기 값은 y 증가량 / x 증가량 = 2 / 1 = 2 다. 그리고 y 증가량과 x 증가량이 양의 방향이므로 기울기는 양의 값을 가진다. 학습율은 항상 양의 값이다. 위 공식을 전개시킨 결과는 이전보다 작아진 w 값이다.
그래프 상에선 w 점이 점점 왼쪽으로 이동하는 형태이고 cost function J(w) 함수를 최소화시키는 목표와 부합한다.
이제 다른 예제를 살펴보자. 이제 위 그림과 다르게 수렴하는 구간 왼쪽 편에 있는 w 값을 선택했을 때의 상황을 보자.
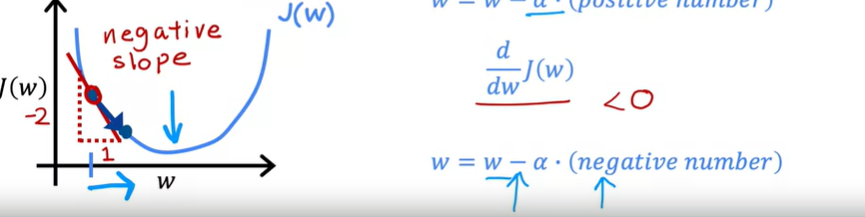
위 경우 탄젠트 값, J 함수의 미분계수, 기울기는 하향하는 음의 값을 가지는 것을 확인할 수 있다. 높이가 2라고 한다면 y 증가량 / x 증가량 = -2 / 1 = -2 가 된다. 위 공식을 전개시킨 결과는 이전보다 커진 w 값이다.
그래프 상에선 w 점이 점점 오른쪽으로 이동하는 형태이고 cost function J(w) 함수를 최소화시키는 목표와 부합한다.
이를 통해서 gradient descent 공식에서 J 함수의 미분계수가 무엇을 의미하는지, 이 값이 gradient descent 값을 어떻게 변경시켜 최소화된 값을 얻는지를 확인하였다.
이제 다른 변수인 알파(학습율)에 대해서 알아보도록 한다.
학습율 값을 어떻게 정하느냐에 따라 gradient descent 알고리즘의 효율성이 정해진다.
학습율을 배우기 위해, 학습율 값이 너무 작을 때 혹은 클 때 어떤 일이 발생하는지 알아보자.
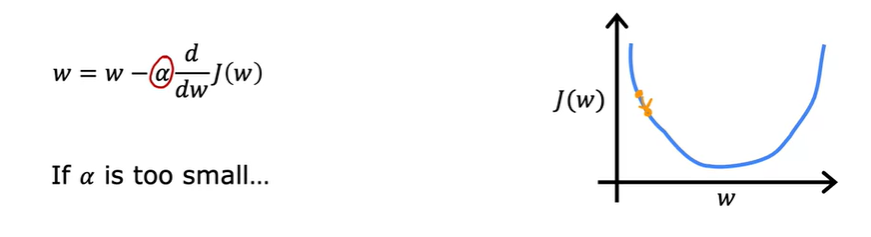
만약 학습율을 매우 작게 0.0000001 로 설정한다면, 위 점에서 다음 점으로 이동할 때의 스텝은 매우매우 작다. 마찬가지로 그 다음 스텝도 매우 작다. 결과적으로 아래 그림과 같이 그려진다.

cost function J(w) 함수 값을 최소화 시켜나가면서 minimum 값에 다다르지만 매우 느리게 진행이 된다.
정리하면, 학습율 값이 작을 경우 gradient descent 는 매우 느리게 동작을 한다.
만약 학습율을 매우 크게 설정한다면 어떻게 될까?

위 그림과 같이 좌측의 분홍점에서 학습율이 큰 graident descent 알고리즘을 동작시켜 minimum 값을 찾는다고 해보자.
그러면 매우 큰 스텝으로 다음 점에 다다르게 되면서 결과적으로 아래 그림과 같이 그려진다.

각 점을 이동할 때마다 점진적으로 더 큰 스텝으로 이동이 되기 때문에 minimum 값에 다다를 수 없게 되고 결과적으로 수렴이 되는 대신 발산될수도 있다.
이제 응용 예제를 하나 살펴볼텐데 해당 케이스는 까다로운 측에 속한다.
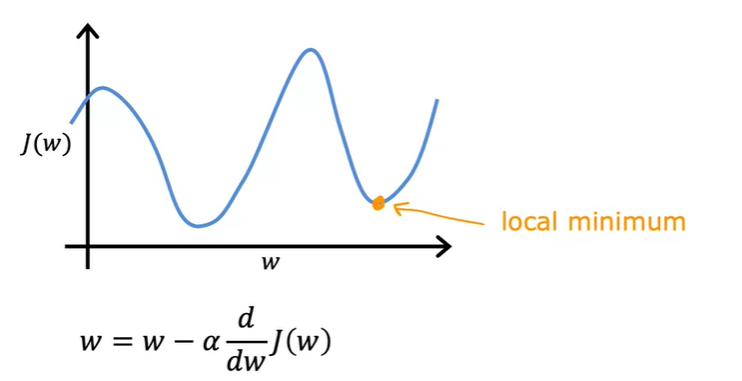
위 J(w) 함수는 2개의 local minimum을 가지고 있다.
만약 위 그림처럼, 이미 local minimum 지점에 도달했을 때 gradient descent 는 어떻게 동작할까?
만약 해당 local minimum의 w 값이 5라면 이때의 탄젠트 값, 기울기는 0이다.
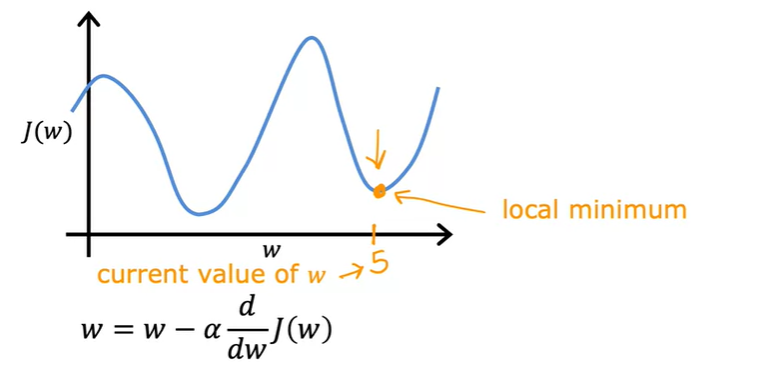
결과적으로 위 공식은 w = w 로 치환이 되고, w 값의 변화는 없어지게 된다.
정리하면, local minimum에 도달하게 될때 gradient descent는 w 값을 변경하지 않는다.
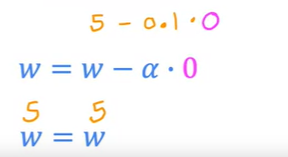
위 사실은 고정된 학습율값을 통해서도 local minimum 값을 구할 수 있다는 것을 의미한다. 아래 그림을 보자.
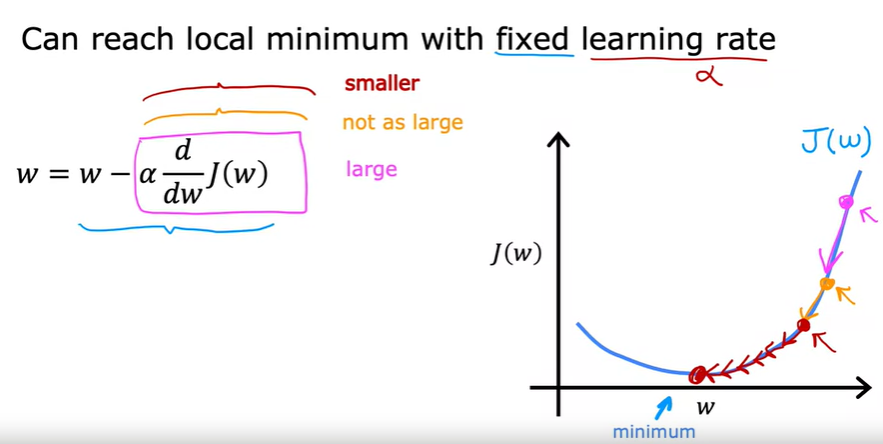
맨 처음 우측의 점에서 다음 점으로 이동할 때는 큰 스텝을 밟는다. 그 다음 스텝에서 다음 스텝을 밟을 때 기울기가 크지 않는데 이는 J함수의 미분 계수 값이 크지 않다는 것을 의미한다. 그 다음 스텝은 더 작아진다.
minimum 값에 가까워 질수록 J함수의 미분 계수값은 점점 0에 가까워진다.

정리하면, gradient descent 알고리즘을 사용해서 minimum 값에 다다를 경우 점점 더 작은 스텝을 밟게 되고(J함수의 미분계수 값이 점점 더 작아지고), 해당 과정을 minimum 값을 구할때까지 반복한다.
위 방식은 최소화된 크기의 cost function 을 찾기 위해서 사방팔방으로 사용할 수 있다.
이제 앞서 배웠던 학습율과 cost function을 통해서 우리의 첫 머신러닝 알고리즘을 만들어보도록 하자.
'머신러닝 > Coursera 강의 정리' 카테고리의 다른 글
| 2주차 강의 내용 정리 - 1 (0) | 2023.07.19 |
|---|---|
| 1주차 강의 내용 정리 - 7 (0) | 2023.07.18 |
| 1주차 강의 내용 정리 - 5 (0) | 2023.07.06 |
| 1주차 도입부 - What is machine learning? (0) | 2023.06.18 |
| 1주차 강의 내용 정리 - 4 (0) | 2023.03.14 |




댓글