개요
1주차 내용을 이어서 정리합니다.
Cost function
지난 시간에 배운 것을 Recap 한다.

- Model 을 사용할 때 parameter 인 w,b 가 있고 w,b 를 구하기 위해 cost function 을 사용한다. 이때 cost function 의 규모를 최소화 시키는 w, b 값을 찾는다.
- 오른쪽 형태는 b가 0이라고 가정하여 함수를 간단하게 표현한 것이다. 이 경우 cost function J(w)는 위와 같이 표현이 되고 원점을 통과하는 선이 그려진다. 마찬가지로 cost function의 규모를 최소화 시키는 w 값을 찾아야 한다.
원점을 통과하는 예제를 계속 살펴보자.
Model 을 나타내는 fw(x) 함수 및 cost function 을 나타내는 J(w) 함수를 서로 대칭하면 아래와 같다.
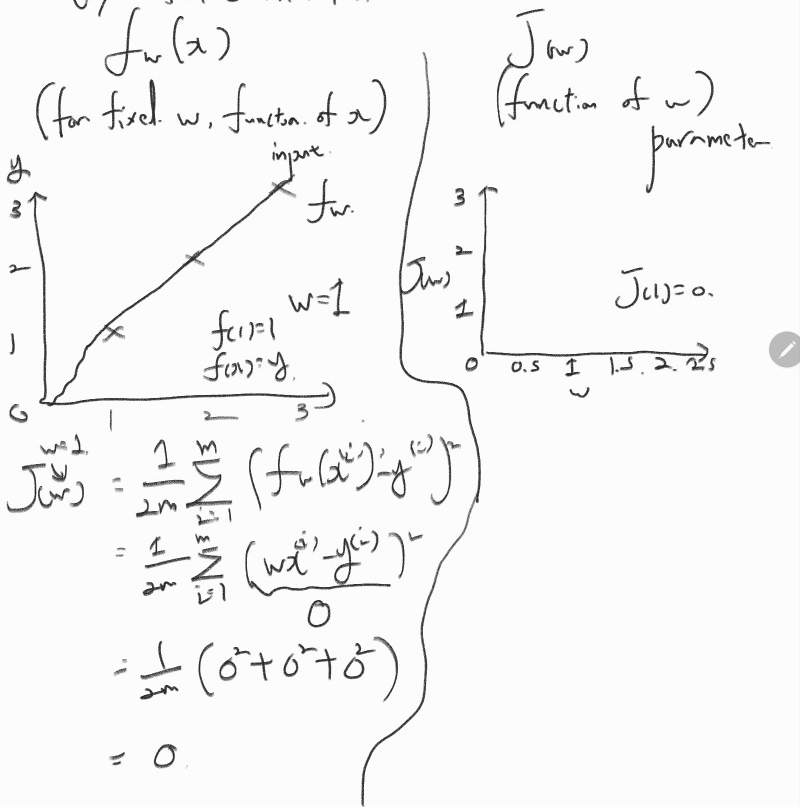
training set 과 Model 이 예측한 값 사이의 간격, 오차는 fw(x) 함수에서 확인할 수 있다.
위 케이스의 경우 w = 1 일때를 가정하여 fw(x) 그래프를 그렸다. 표현식을 전개하다보면, wx^(i) - y^(i) 로 나타낼 수 있는데 결과는 0이다. 왜냐면 x = 1일때 y = 1고, x = 2일때, y도 2가 되기 때문이다. 나머지 값들도 마찬가지다.
결과적으로 f(x) = y 라는 표현식으로 나타낼 수 있다.
그래서 cost function 의 값은 0이다. Model의 예측값이 정확하다는 것을 의미한다고도 볼 수 있다.
우측의 J(w)를 다시 표현하자면 w = 1 인 경우, J(1) = 0 으로 나타난다.
이제 w = 0.5인 경우를 살펴보자.

위 경우에 대해 cost function 식을 적용하여 얻은 cost function의 값은 0.58 이다. 오차 값이 대략적으로 0.58 이란 것이다.
구한 cost function 값을 오른쪽에 J(w) 함수에 찍으면 위와 같다.
만약 w = 0 인 경우에는 cost function은 대략 2.3 이라는 값이 나온다. w 가 -0.5 인 경우는 대략 5.25 라는 값이 나온다. 이런식으로 w 에 대하여 수 많은 값을 대입할 수 있다.
이렇게 서로 다른 w 값을 대입한 예제들을 통해 알 수 있는 것은 b = 0인 J(w) 함수는 아래와 같이 포물선을 그린다.

w 를 적용했을 때 왼쪽, 오른쪽의 그래프에 어떤 형태로 그림이 그려지는지에 주의깊게 볼 필요가 있다.
오른쪽 그래프에서 구한 w 값들은 왼쪽 그래프에서 나타난 각각의 선들을 통해 구해진다. 다시 말해 주어진 학습 데이터에 밀착되게끔 그려진 왼쪽 그래프의 각각의 선은 오른쪽 그래프의 각 점에 해당한다.
위 그림 오른쪽의 J(w) 그래프를 통해 w = 1을 고르면 training data sets 와 매우 일치하는 Model 예측값을 얻을 수 있다.
정리하면, linear regression 에선 다양한 w 값들을 대입하여 cost function의 최소화 값을 찾는데, 이는 데이터와 가장 밀착하는 선을 그리는 것을 의미한다. 그래서 제곱된 오차를 최소화하는 w 값을 찾는 것이 좋은 모델을 찾을 수 있는 관건이다.
결론: linear regression의 목표는 가장 최소화된 크기의 cost function J(w) 를 갖는 w, b 값을 찾는것이다.
'머신러닝 > Coursera 강의 정리' 카테고리의 다른 글
| 1주차 강의 내용 정리 - 5 (0) | 2023.07.06 |
|---|---|
| 1주차 도입부 - What is machine learning? (0) | 2023.06.18 |
| 1주차 강의 내용 정리 - 3 (0) | 2023.03.13 |
| 1주차 강의 내용 정리 - 2 (1) | 2023.03.08 |
| 개요 및 1주차 강의 내용 정리 - 1 (0) | 2023.03.04 |




댓글