개요
지난 시간에 이어서 cost function 에 대해서 다룰텐데, 좀 더 많은 예제를 통해 익힐 것이다.
내용
지난 시간에 배웠던 cost function 개념의 전반적인 내용을 정리하면 아래와 같다.
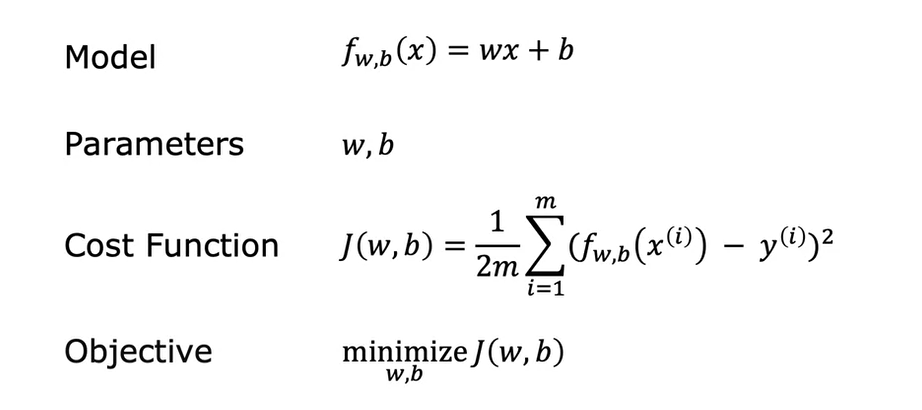
지난 시간에는 b를 0으로 세팅하여 간편하게 구했으나 이번엔 b에 다양한 값을 세팅하여 어떤 형태로 그려지는지 확인해보자

예를 들어 w = 0.06 이고 b = 50 인 f(x) 함수를 그린다고 했을 때 왼쪽 위 형태와 같이 나타내진다. 이 경우 데이터들과 그닥 밀착되어 있지 않으므로 좋은 linear regression model이 아니다.
그리고 이 경우 J(w) 함수는 단순히 이차원 포물선 함수가 아닌 삼차원으로 그려진다, 왜냐면 b의 값이 0이 아닌 값으로 대입되기 때문이다.
그래서 그림은 아래와 같이 나타내진다.
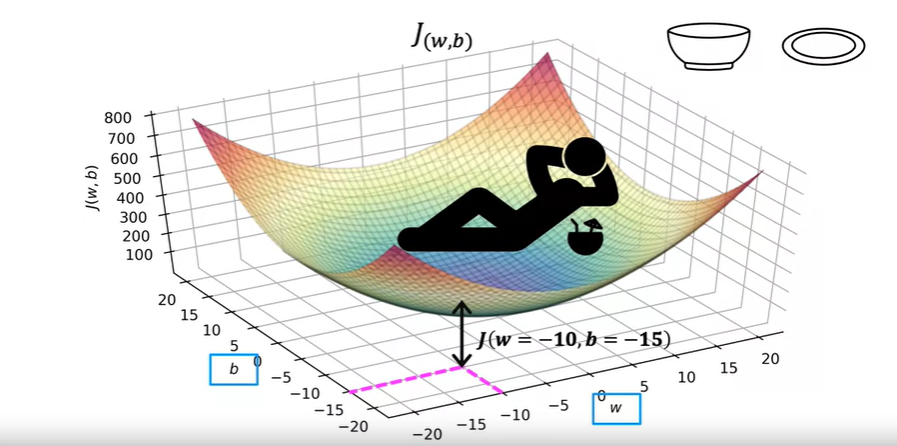
이러한 삼차원 포물선에서 찍히는 각 점의 값은 w, b 값에 따라 달라진다.
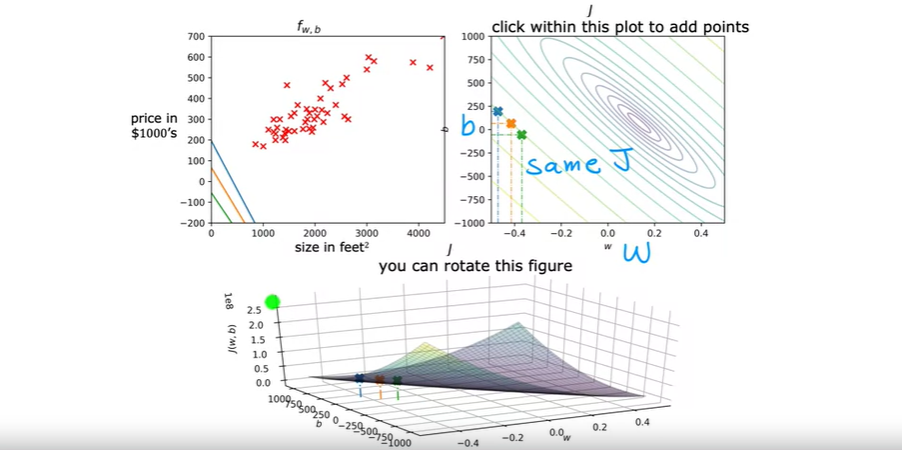
상단 오른쪽의 그래프는 하단의 3차원 cost function을 등차선 그래프로 나타낸 것이다.
상단 오른쪽 그래프의 타원은 3차원 그래프의 점들이 같은 높이에 있다는 것을 보여준다. 위 그림의 상단 오른쪽 그래프에서 볼 수 있듯이 각 점들의 w, b는 다르지만 같은 그래프에 위치해있다. 이는 한마디로 같은 cost function J값을 가진다는 것이다. 또한 각 점들의 f 함수 형태는 다르게 나타난다.
삼차원 그래프를 수평적으로 슬라이스 했을 때 나타나는 그림은 상단 오른쪽 그래프의 각 타원형의 그래프를 나타낸다고 볼 수 있다.
이렇게 등차선 그래프를 사용해서 cost function을 3D로 편리하게 표현할 수 있다는 것을 배웠다. 이제 linear regression model을 사용하면서 세팅했던 w, b값들에 대해 시각화 작업을 해보자, 이를 통해 어떤 w, b 값을 선택하느냐에 따라 f 함수의 선이 학습 데이터들과 잘 밀착되는지 확인할 수 있다.
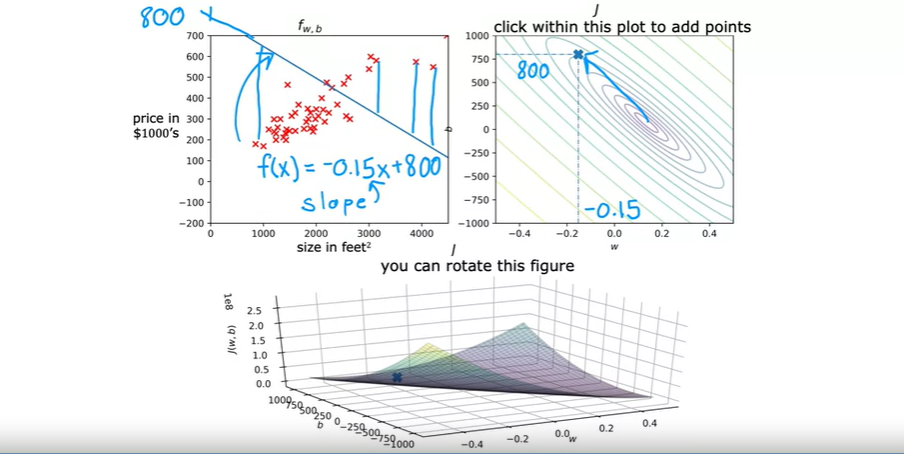
또 다른 예제를 한번 살펴보도록 하자. 오른쪽 J 그래프에 찍힌 점은 왼쪽 fw,b 그래프의 하향하는 선 형태로 표현될 수 있다.
w, b 값은 각각 -0.15, 800 이다. 방정식으로 표현하면 f(x) = -0.15x + 800 이다. 현재 아래 그림에서 나타난 모델의 경우 예측값들이 실제 학습 데이터 값들과 오차가 큰 편이라 좋은 모델이라고 할 수 없다. J 그래프에 찍힌 cost function 값의 경우 최소값(minimum cost) 으로 표현되는 center 타원위치로 부터 많이 떨어져 있는 것을 확인할 수 있다.
또 다른 예제를 살펴보자. 아래 예제는 중심 타원에 가까이 위치한 w, b 를 그래프로 표현한 예제이다.
이 경우 w, b는 0.13, 71 이다. 방정식으로 표현할 경우 f(x) = 0.13x + 71 이다.

위 예제의 fw,b 그래프에서 나타내진 선을 보면, 이 경우 오차 총합의 제곱값은 앞서 봤던 예제의 하향 선보다 가능한 최소화된 값이 나오는 것을 확인할 수 있다.
다음 시간에 배울 gradient descent는 우리가 일일이 Jw,b 그래프에 최적화된 선을 찾지 않아도 되게끔 도와주는 기능을 한다, 한마디로 실전에 바로 적용할 수 있는 최적의 w, b 값을 자동으로 찾아주는 효율적인 알고리즘이다.
'머신러닝 > Coursera 강의 정리' 카테고리의 다른 글
| 1주차 강의 내용 정리 - 7 (0) | 2023.07.18 |
|---|---|
| 1주차 강의 내용 정리 - 6 (0) | 2023.07.12 |
| 1주차 도입부 - What is machine learning? (0) | 2023.06.18 |
| 1주차 강의 내용 정리 - 4 (0) | 2023.03.14 |
| 1주차 강의 내용 정리 - 3 (0) | 2023.03.13 |




댓글