목차
- 개요
- 전체적인 흐름
- Post Process
개요
CSS 코드스피츠 4강 강의를 듣고, 내용을 복습하고 정리하는 차원에서 글을 작성하였습니다. 해당 강좌를 학습하시는 분들께도 도움이 되었으면 합니다.
전체적인 흐름
먼저 Post process 라는 추가적인 단계가 geometry, fragment 단계 외에도 존재하는 것을 배웁니다. 그리고 CSS 속성 중 transform 내에서 3D 속성을 줄 수 있는 perspective, perspective-origin, transform-style, transform-origin, backface-visibility 에 대해 배웁니다. 그리고 실습 예제로 드럼통을 만들어 봅니다. 3D를 구현하려면 2D 보다 더 많은 개념이 필요합니다. 특히 수학적인 개념이 많이 요구되는데 CSS 는 수학적인 개념이 없어도 3D 관련된 도구들을 쉽게 사용할 수 있도록 해주었습니다. 그래서 수학적인 개념은 차치하더라도 사용 방법들을 제대로 알 필요가 있습니다.
Post Process
지금까지 배운 Graphics pipeline은 두 단계가 있습니다. geometry(1단계)와 fragment(2단계) 인데 여기서 pipeline의 의미는 다음과 같습니다.
- Pipeline : 한 데이터 처리 단계의 출력이 다음 단계의 입력으로 이어지는 형태로 연결된 구조를 가리킨다.
여기서 말하는 Graphics pipeline이란 영역을 잡은 후(geometry) 화면에 그림을 그리는(fragment) 작업을 의미합니다.
한편 geometry 과정을 reflow라고도 부르고 fragment 과정을 repaint 라고도 부릅니다. 만약 geometry, 즉 reflow를 다시 하면 영역 전체를 다시 잡은 뒤 색칠도 다시 해야되기 때문에 비용을 많이 먹습니다. 그러므로 되도록이면 repaint 만 하는 최적화 기법을 사용하길 권장합니다.
이 후 Graphics pipeline에 Post process 라는 과정이 하나 더 추가되었습니다. Post process는 브라우저가 geometry, fragment 단계를 거친 다음 바로 색칠을 하도록 하는게 아니라 한번 더 가공할 수 있는 찬스를 주는 추가 과정입니다.
그림으로 한번 더 살펴볼까요?
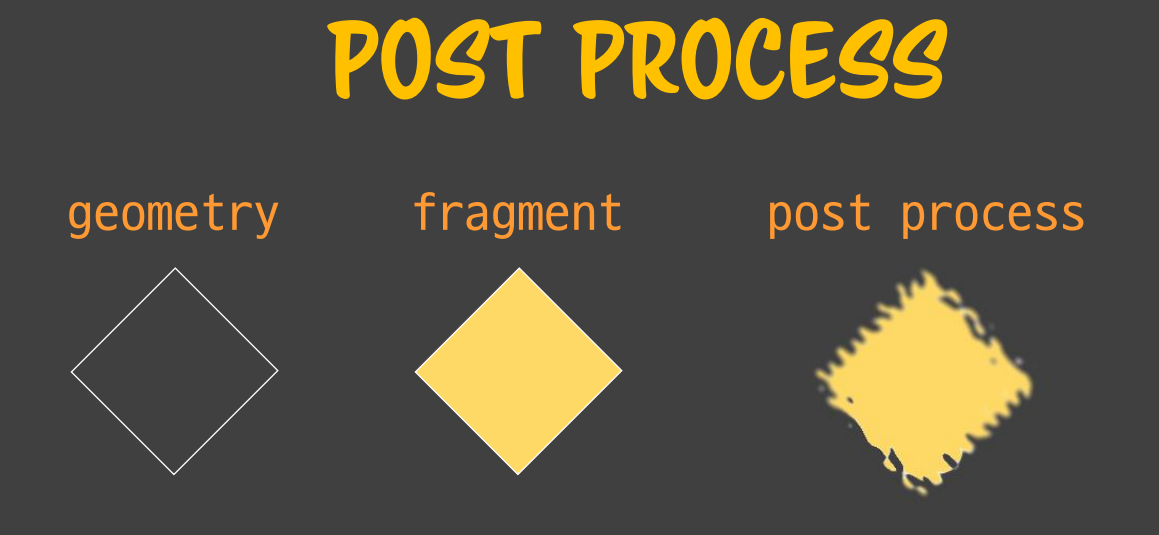
Geometry 단계 : 다이아몬드 형태로 영역을 잡음
Fragment 단계 : 내부를 노란색으로 칠함. 이 단계에 이르러 무슨 색으로 칠할 지 알 수 있을 정도로 완성되어 있는 pixel 데이터가 됨.
그런데 여기에 Post process 라는 후 변형 작업 을 더 거칠 수 있습니다.
Post process : ripple, blur 같은 수학적 공식(=CSS 속성)을 통해서 완성되어 있는 pixel 값을 변형시킴
Post process 단계는 geometry, fragment 단계와 관련없이 따로 진행됩니다. 이게 무슨 뜻일까요?
우선 Post process 단계를 거치기 위해서 쓰는 Buffer 라는 메모리 개념에 대해 먼저 알아봅시다. Buffer는 x, y에 해당되는 점을 찍어놓고 해당 위치 색깔을 기억하고 있는 2차원 배열입니다. 그래서 geometry 단계에서 계산을 한 뒤 바로 Graphic bitmap 에서 쓰는 것이 아니라 우선 Buffer 메모리에 저장을 하고 여기서 조작을 한 뒤에 그림을 그리게 됩니다.
(graphic bitmap이 무슨 뜻인지 검색 필요)
기존 브라우저에선 Buffer라는 개념이 없어서 fragment 단계까지만 처리가 되었지만 IE 5.5 부터는 Buffer 개념을 도입하여 그림을 그린 뒤부터는 모든 브라우저가 직접 그림을 그리지 않고 buffer를 사용하여 그림을 그리게 되었습니다.
이 buffer 배열에 있는 것들만 위 사진의 Post process 단계 그림처럼 변형을 한 뒤에 비로소 그림을 그리기 시작합니다.
예전에는 그림을 CPU가 graphics pipeline 단계를 거쳐 그려줬지만 지금은 GPU(Graphic processing unit)가 대부분의 그림을 그립니다. 이 때 GPU가 그림을 그리려면 CPU가 만들어낸 이미지를 GPU에 올려줘야합니다. CPU가 데이터를 잘 가공해서 GPU 에게 넘겨줘야지만 그림을 그릴 수 있기 때문입니다. 굳이 GPU가 그림을 그리지 않고, CPU가 가공을 한뒤 바로 그림을 그릴 수도 있지만 GPU의 속도가 훨씬 빠르기 때문에 GPU가 처리하게끔 합니다.
그래서 모던 브라우저에서는 CPU를 이용해서 geometry를 계산하고, 기본 fragment 를 채운 뒤 가공된 buffer를 GPU에게 넘겨 GPU에서 Post process를 처리하게 합니다. 이런 단계를 거쳐 현재 우리가 보는 화면이 그려집니다. (~5:44. Post process 가 정확히 무엇을 의미하는 건가요? Buffer 를 변형하는 작업? 혹은 Buffer를 받고 이것을 다시 변형해서 그리는 작업?)
또 CSS 키워드는 종류에 따라 CPU에서 처리하기도, GPU(Post process)에서 처리하기도 합니다. 그러나 무조건 GPU를 쓴다고 좋은 것은 아니기 때문에 각 CSS 속성들을 처리하기 위해 CPU와 GPU의 사용을 양분합니다. 이를 통해 Machine의 전체 성능을 끌어내어 Graphics 를 처리할 수 있습니다!
추가적으로 메모리와 관련해, Graphics는 다른 데이터들에 비해 (ex. 서버 데이터 = 수십 KB)에 비해 메모리를 먹는 양(수 MB~)이 가장 크기 때문에 처리를 위해 고용량 메모리를 사용합니다. (+ 그만큼 다루기도 어렵습니다.)
현대의 컴퓨터 언어 대부분은 Garbage Collector 라는게 있어서 안 쓰는 메모리가 있으면 사용자가 직접 처리를 하지 않아도 알아서 찾아서 없애줍니다. 그럼에도, 대부분 언어들이 유일하게 bitmap 데이터만큼은 즉시 해제할 수 있는 메소드를 제공해줍니다. 왜냐면 메모리를 많이 차지하기 때문입니다. 화려한 UI를 제공하는 사이트(ex. BMW 프로모션 사이트)들에는 대부분 밸런스를 잘 조절하여 CPU와 GPU가 각각 어디까지 처리를 하게끔 정리해놓습니다.
Post process를 사용하는 대표적인 CSS 속성들은 Transform, Keyframe animation 등이 있습니다. 이들은 CPU가 아닌 GPU를 사용해서 처리하기 때문에 사용할 시점에는 CPU가 상대적으로 널널해지고 그에 따라 javascript 코드가 돌기 편해집니다.
그림을 보면서 앞서 얘기한 세 가지 단계를 현실적으로 살펴볼까요?
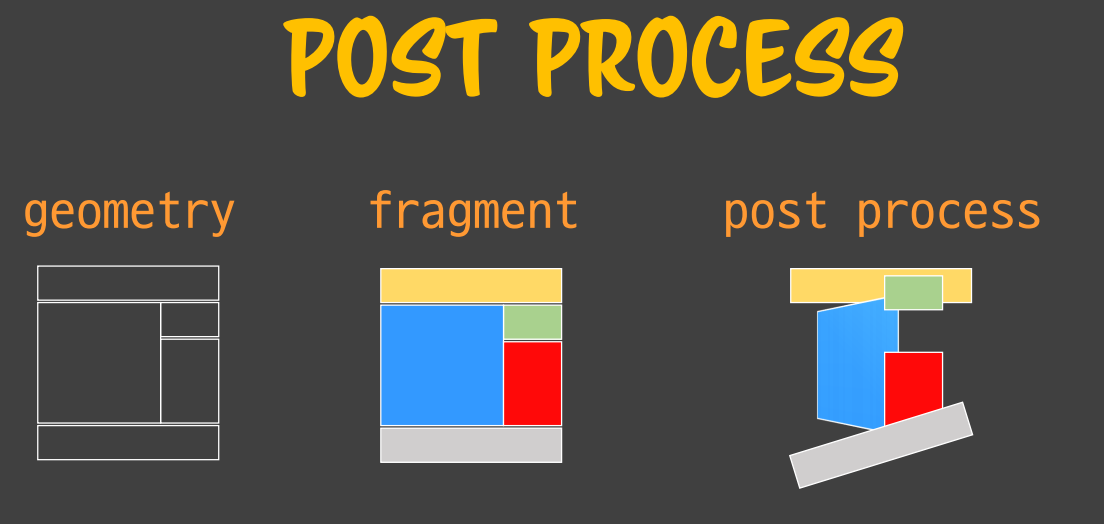
1. 먼저 div 태그에 float, absolute 등의 속성을 주면서 geometry 를 그립니다.
2. 색깔을 주고, 텍스트를 넣으며 fragment 를 색칠합니다.
3. Transform 과 같은 css 속성을 추가로 주면 fragment 단계의 각각 element들을 위 사진처럼 변형 합니다.
GPU에게 넘어왔을 땐 post process 이전 단계까지 있던 요소들(div, body 등의 태그)이 `<div></div>` 와 같은 텍스트로 보이지 않고 전부 이미지로 보이게 됩니다. 그러면 사진에서 보는 것처럼 하나하나 요소들을 각각의 이미지로 바라보고 blur 효과 등을 줄 수 있습니다.
GPU와 CPU에 부하를 나누어서 처리를 할 수 있고, Post process는 우리가 원하는 화면을 CPU, GPU가 서로 나눠서 처리할 수 있게 합니다.
CSS에서 3D와 관련된 모든 처리는 전부 GPU(Post process)가 합니다.
기억해야 할 것은 3D를 주기 전 상황(fragment 까지 단계)과 3D를 준 이후 상황(Post process 단계)는 서로 아무런 상관이 없습니다. Post process 단계에선 그림만 바꾼 것이기 때문에(그림만 바꾼 것이라는게 무슨 말인지 잘 모르겠어요..) DOM 구조와 아무런 상관이 없습니다. post process는 float, absolute, relative 계산 등이 fragment 단계에서 모두 처리된 상태에 대하여 받는 것입니다.

3D와 관련된 첫번째 속성을 살펴보겠습니다. 먼저 '원근' 이라는 뜻을 가진 perspective 라는 속성이 있습니다.
(원근 : 멀고 가까움)
이 때 원근의 거리는 컴퓨터 모니터와 사람의 눈 사이에 거리를 의미하며, perspective:600px 로 준 것은 잠정적으로 그 거리가 600px 만큼 떨어진 것을 의미합니다. 그래서 같은 사물이라도 perspective 값을 갈수록 더 크게 준다면 그 사물은 원래 보이던 것보다 점점 더 작게 보입니다.
또한 perspective 값을 시야로부터 가깝게 줄수록 왜곡 효과가 굉장히 커집니다. 예를 들어, 어떤 사람이 나로부터 대략 500px 정도 떨어져 있습니다. 이 때 내 시야로부터 그 사람의 머리나 어깨를 보았을 때 둘 다 똑같이 멀리 느껴지고 평평하게(2D그림처럼) 보입니다. 그러나 가까이 다가섰을 때 내 눈에 좀 더 가까운 머리는 크게 보이지만 어깨 부분은 그보다 작아보이는 현상이 있습니다. 이를 '어안렌즈 효과' 라고 하며 가까이 다가섰을 때 내 시야로부터 그 사람의 머리, 어깨까지의 거리가 각각 10px, 15px 이라고 했을 때 단지 5px의 차이가 날뿐인데도 굉장히 크게 느껴지는 것입니다.
가까이 있을수록 3D로 쉽게 느낄 수 있지만 멀리 있을수록 3D인지, 2D 인지 크게 구분이 안되고 2D로만 보이게 되는 현상이 있습니다. 동시에 가까이 갈수록 3D의 왜곡효과는 커집니다. 그래서 perspective 효과를 길게 주느냐, 짧게 주느냐는 왜곡에 대한 정도를 나타내기도 합니다.
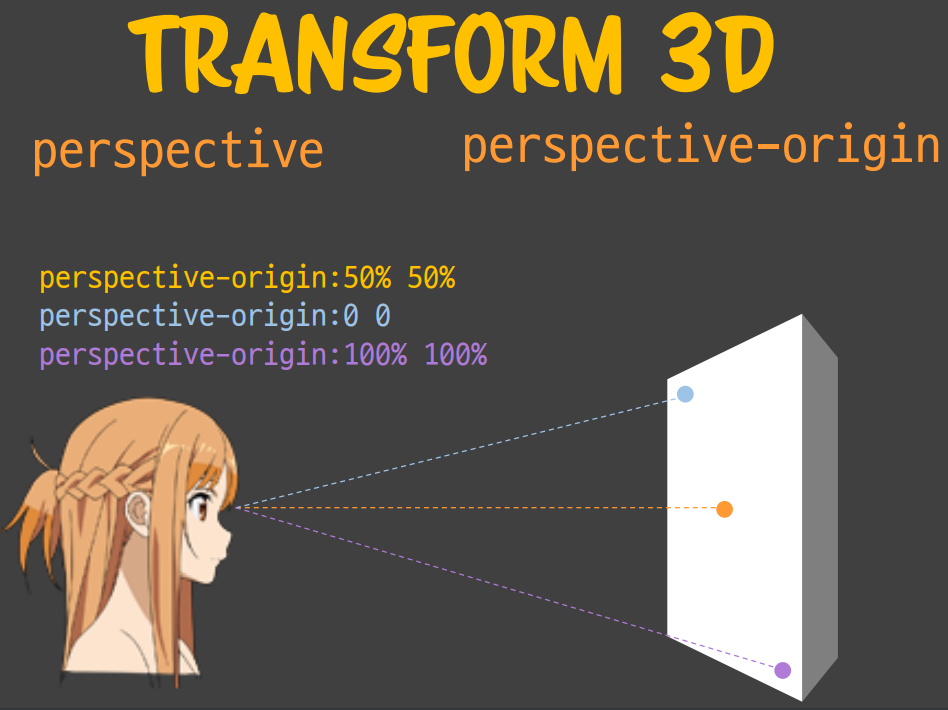
이어서 perspective-origin이라는 개념이 있습니다 (transform-origin 과 비슷한 의미입니다) perspective-origin 이란우리의 눈으로 바라볼 때 어느 위치를 바라볼 것인지에 대한 기준점입니다. 다른 말로는 변형을 줄 때 어디를 바라보고 3D로 인식할 것이냐 를 의미합니다. 기존에 perspective 거리를 준 것은 모니터 한 가운데를 바라보고 있다는 것이 가정되있었습니다. 그런데 사진처럼 origin 을 좌상단 또는 우하단으로도 줄 수 있으며 값을 (50% 50%)으로 주면 가운데를 바라볼 수 있습니다. 이에 따라 왜곡을 주는 point또한 달라지는데, 가운데를 바라보면 가운데가 가장 왜곡이 덜 되고 좌상단 우하단에 왜곡이 많이 가해질 것이며 우하단을 바라보면 좌상단에 가장 크게 왜곡이 가해질 것입니다.
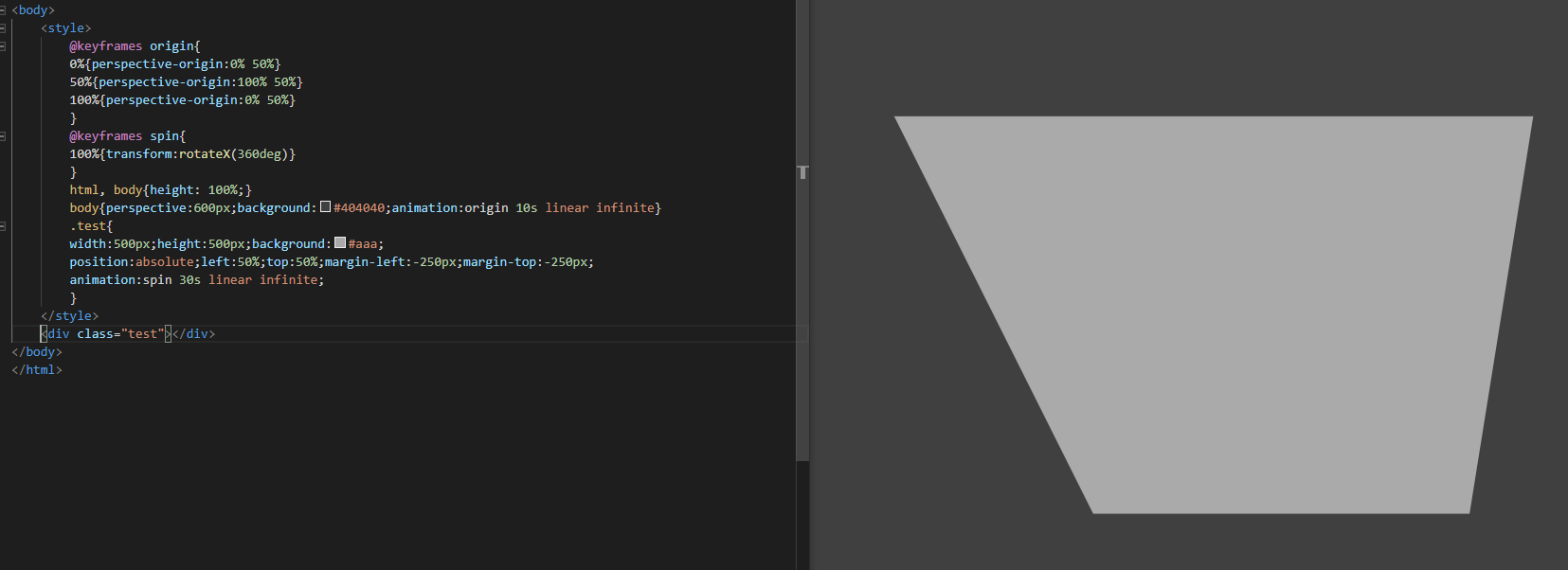
예제로 주어진 코드를 살펴보면 body에 perspective를 600px로 주고 x축 방향으로 360도 회전을 하게끔 되어있습니다. 그리고 origin 이라는 animation 속성은 perspective-origin을 계속 변형하고 있습니다. 실제로 실행을 하면 정사각형이 3D 그림이 회전을 하듯 도는 것을 볼 수 있습니다. 실제론 x축을 360도 회전만 할 뿐인데 3D 형태로 회전하는 것처럼 보이는 것은 왜곡점이 달라져 보이기 때문에(perspective-origin이 변화) 생기는 것이고, 왜곡점이 달라져 보이는 이유는 우리가 바라보는 눈의 위치를 자꾸 바꾸기 때문에 회전하는 것처럼 보이게 됩니다. 원근 왜곡은 perspective 값을 주는 순간부터 시작됩니다.

이제 transform-style 이라는 것을 배우겠습니다. 그전에 한 가지 질문이 있습니다.
div 태그가 위 그림과 같은 구조로 되어있다고 할 때 '앞서서 fragment 단계까지 존재한 DOM의 계층 구조가 GPU로 넘어간 후 그려질 3D 정보들 사이에서 영향을 미치는가?' 혹은 '부모 div가 회전할 때 자식의 div 또한 같이 회전이 되는가?' 입니다.
한 마디로 부모의 3D 속성(perspective, 3D x/y/z, rotateX/Y/Z, scaleX/Y/Z 등)를 자식이 그대로 이어받길 원합니다. 오른쪽보단 왼쪽 그림이 되길 원하는 것이죠. transform-style:flat 으로 하면 오른쪽 그림처럼 되고, transform-style:preserve-3d로 하면 왼쪽 그림처럼 됩니다 (flat은 기본값입니다)
그래서 transform-style은 post process(GPU) 에게 DOM tree 구조를 반영해서 3D를 그릴 수 있게 하는 속성입니다. preserve-3d 를 주었을 때 자식이 부모의 3D 속성을 이어받게되고 이를 GPU 가 그림을 그리게 됩니다.
이제 transform-origin 을 살펴보겠습니다. perspective-origin이 우리가 눈으로 바라볼 때 위치라는 개념이었다면 transform-origin은 실제 변형이 일어날 때 위치를 어디로 정할 것이냐 를 의미합니다.
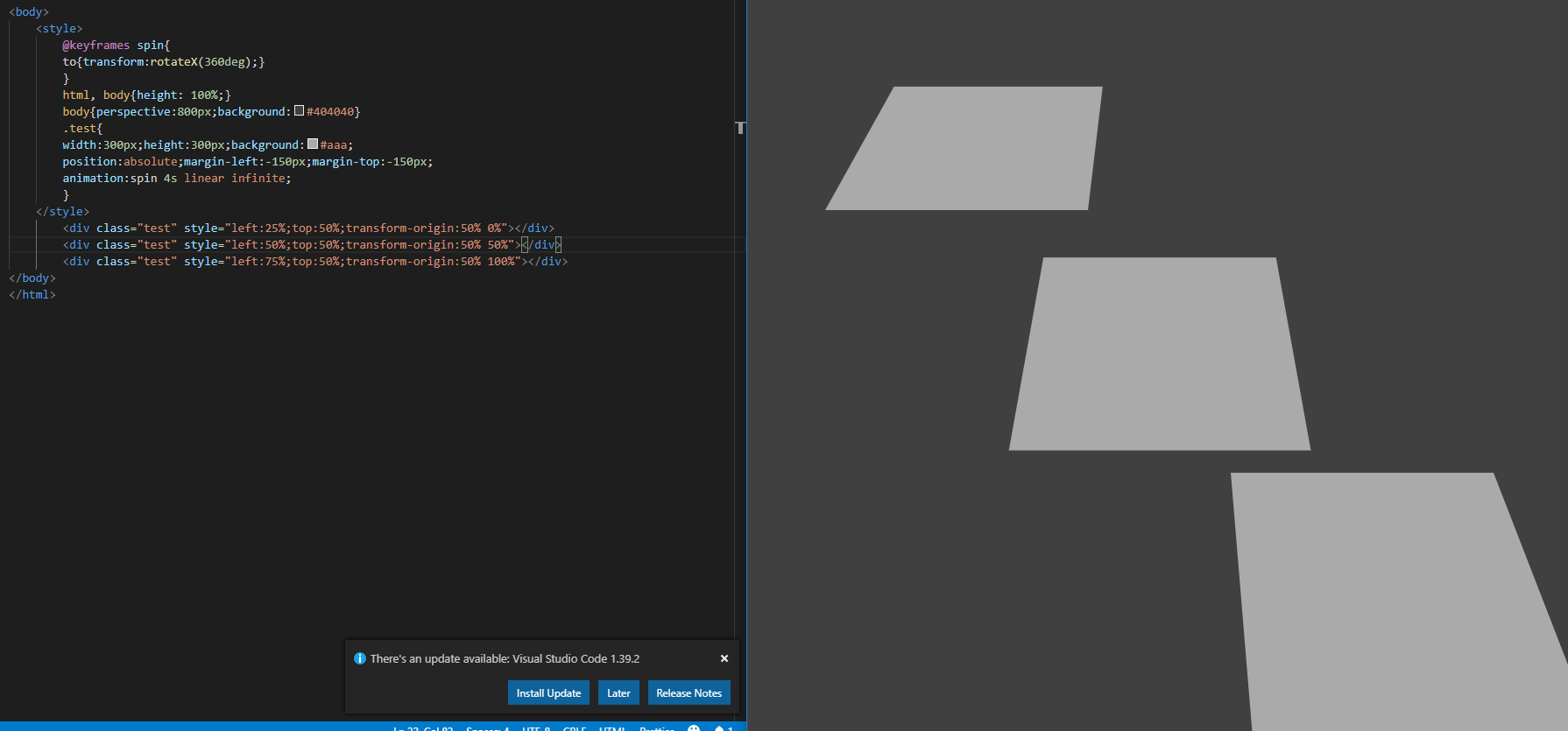
transform-origin에 들어가는 값의 순서는 X, Y, Z 입니다. 만약 값을 50% 50% 을 주면 가운데를 변형이 일어날 기준으로 잡고 50% 100% 를 주면 맨 하단을 변형이 일어날 기준으로 잡습니다. 그래서 예제 코드를 돌릴 때 각각 사각형은 맨 상단, 가운데, 하단을 기준으로 잡고 회전을 하고 있습니다.
여러분들이 3D 관련 속성들을 봐도 오래 기억하지 못하는 것은 각각을 단편적으로 알고 있기 때문입니다. CSS 3D 속성들 5가지를 하나의 묶음으로 알고 있다면 좀 더 기억하기 쉽습니다.
이제 backface-visibility 를 알아보겠습니다.
backface-visibility 는 요소의 뒷면이 보이게 할지 말지를 결정하는 속성입니다. ( 이 개념과 반대되는 개념은 frontface-visibility 입니다 ) backface-visibility가 왜 필요한지 예를 들며 알아보겠습니다.
앞 뒤가 서로 다른 요소가 있을 때 앞면만 보이게 하면 되고 뒷면은 가려도 됩니다. 예를 들어 각각 빨간색, 파란색인 요소가 있습니다. 이 요소가 일반적으로 빨간색이 보이다가 y축으로 회전해서 뒷면인 파란색이 보이게 될 때 backface를 가리게 해버리는 것입니다. 또 다른 예로 정육면체 3D가 있을 때 바깥쪽만 우리눈에 보이므로 안쪽은 굳이 그릴 필요가 없습니다.
핵심은 앞면과 뒷면이란 서로 다른 frontface를 가진 요소가 서로 합쳐진 형태이며 3D세상에서 그들의 backface는 우리의 눈에 보이지 않는 다는 점입니다. 그런데 일반적으로 컴퓨터는 기본적으로 뒷면마저도 전부 그려버리기 때문에 컴퓨터의 성능상 부하를 줄이기 위해서 뒷면을 안보이도록 설정을 해줘야 합니다 (backface-visibility : hidden) 이렇게하면 컴퓨터는 할일이 반으로 줄게 됩니다.
이 때 backface를 안 보이게 하는 행위를 culling (컬링, 음면처리) 이라고 부릅니다.
이러한 설정이 중요한 이유는 그림을 그리는 작업이 가장 큰 부하를 갖기 때문입니다. 브라우저 프로파일링을 했을 때 렌더링이 95%를 차지하는 것 또한 같은 이유입니다. 그래서 javascript 코드에서 최적화를 sorting을 잘한다고 해도 이는 5% 밖에 차지하지 않기 때문에 큰 변화를 주기 힘듭니다.
프론트엔드에서 쾌적한 화면을 만들기 위해선 그림 그리는 것의 최적화가 가장 중요합니다.
그래서 실제로 자바스크립트 코드를 최적화하면 전체적으로 2% 개선되는데 비해 그림 그리는 것, 렌더링을 개선하면 30%, 50% 씩 크게 개선이 됩니다.
이런 특징을 응용하여 GPU가 3D 관련된 것들을 모두 처리하기 때문에 3D 속성을 줘서 일부로 post process가 처리하게 도 합니다. 예를 들어 rotateX:0 을 특정 화면요소에 임의적으로 대입시키는데 이는 X축으로 돌지 않으므로 아무런 효과가 없지만 3D 속성이므로 GPU가 처리하게 됩니다. 이처럼 언뜻 보기엔 이 속성이 특정 화면 요소에 필요하지 않은데 3D 속성을 줌으로써 CPU가 아닌 GPU가 처리하게끔 넘길 수 있습니다. 이런 기법이 굉장히 많이 사용되고 실제로도 큰 그림들이나 몇개의 그림들을 사이트에 그릴 때 GPU쪽으로 분산시키기 위해 내부 CSS 속성에 rotateX:0 를 넣어줍니다.
지금까지 내용을 정리하면 렌더링 로직 개선하기 위해서 CSS를 사용하고, CSS를 사용할 때 post process, post process 가 아닌 애들끼리 balance를 잘 나눠주는 것이 중요합니다. 그리고 앞서 배운 속성 5가지를 이용하면 원하는 3D효과를 낼 수 있습니다.
지금까지 배운 기본 개념들로 3D 예제를 실습하겠습니다. 이 때 CSS Sprite라는 개념을 익히고 가겠습니다.
CSS Sprite란 여러 개의 이미지를 하나로 합쳐서 서버에 요청하는 비용을 줄이게 해주는 그림을 의미합니다.
3D 세계에선 이 용어를 Atlas라고 부릅니다.
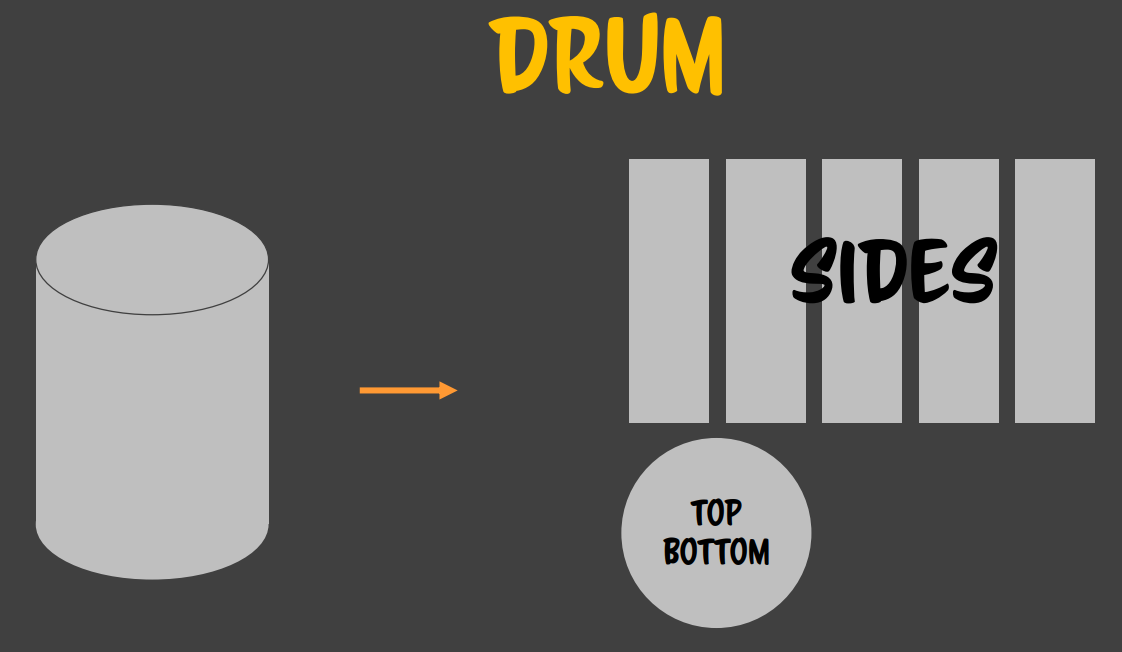
위 사진에서 동그란 원통을 구성하는 직사각형 5개와 원형 하나 등을 각각 face 라고 부르며, 이 face들이 여러 개 합쳐져서 만들어진 것을 mesh 라고 합니다. 각각의 face들은 CSS Sprite로 구성되어 있고 이를 통해 드럼통형태의 mesh를 만들 것입니다.

드럼통은 3D 상에서 좌표를 나타내는 x,y,z 와 높이와 넓이 값인 h, w 값을 주어 만듭니다. 그리고 CSS Sprite로 하나의 이미지를 각각의 pace로 나누어야 하므로 전체 이미지 내에서의 좌표 값인 tx, ty 값 또한 필요합니다. 마지막으로 회전을 시킬 것이므로 rx, ry, rz 값 또한 줄 것입니다. 이런 값들을 준다는 것을 알았으니 이제 직접 class 를 구현해보겠습니다.
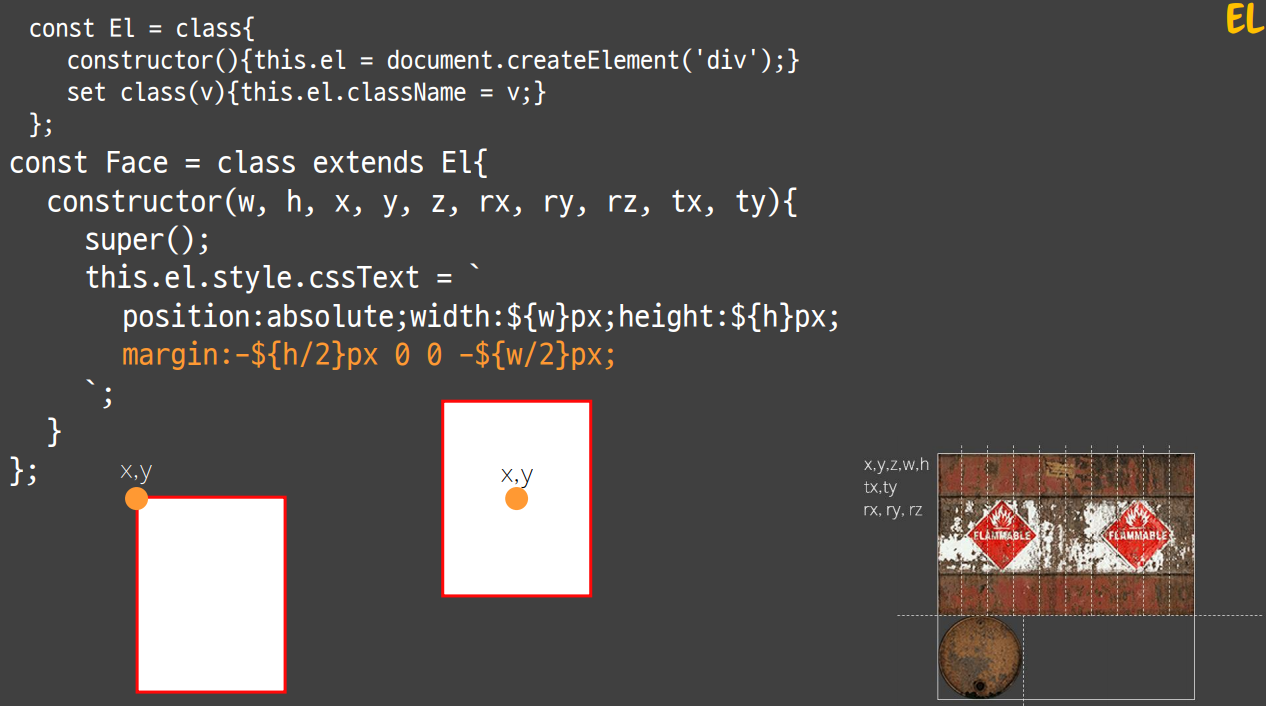
먼저 El 이라는 클래스를 만듭니다. 이 클래스의 용도는 div 라는 element를 생성해주고 class 이름을 넘겨주면 해당 인스턴스의 div 태그에 class 값을 넣어줍니다.
그리고 El 태그를 상속받는 Face 클래스를 만듭니다. Face 클래스는 앞서 얘기한 x,y,z,tx,ty,rx,ry,rz 값들을 인자로 받으며 이 값들을 통해 3D 그립니다. 또 cssText란 속성으로 css 속성들을 한번에 지정합니다. 이 때 position 값에 따라 중앙정렬하는 기법을 설명하겠습니다.
position:absolute를 줬을 때 중앙 정렬을 하고 싶다면 적절히 margin 값을 주면 됩니다.
ex) margin : -${h/2}px 0 0 -${w/2}px;
position:absolute를 주지않았을 때 중앙 정렬을 하고 싶다면 margin-left, margin-right에 auto를 주면 됩니다.
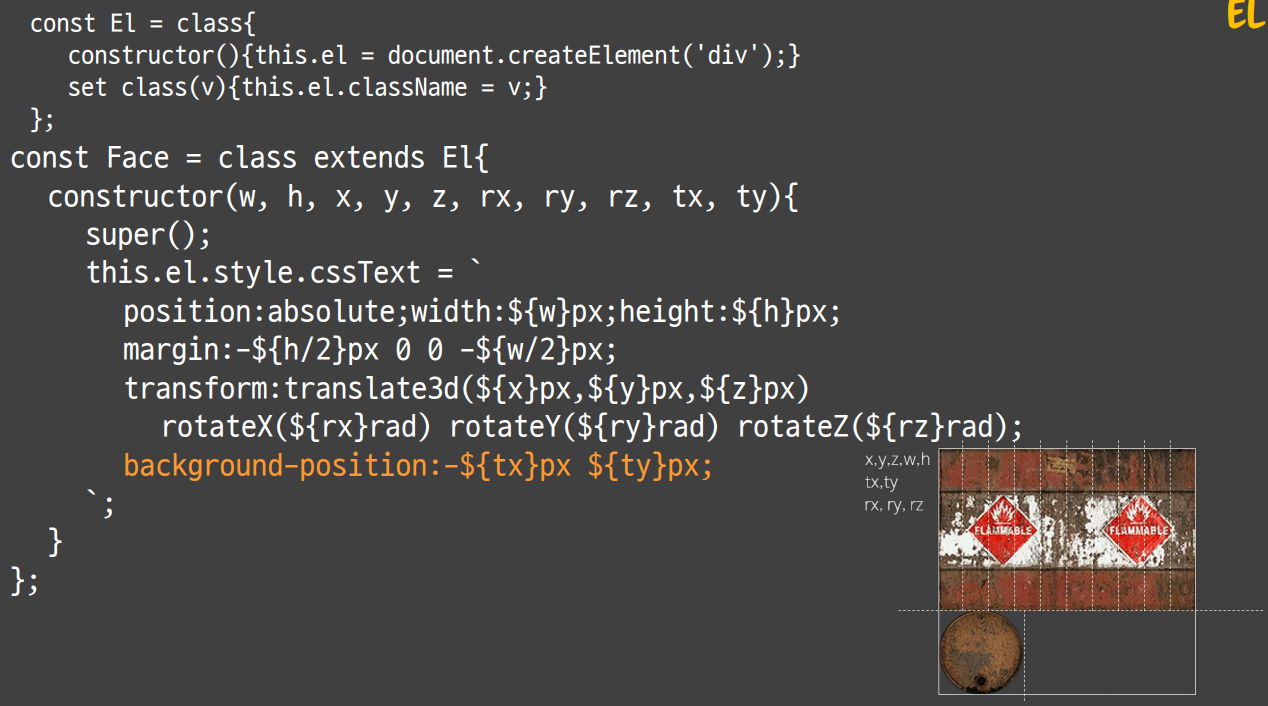
그리고 transform 에 translate3d 메소드를 사용하여 x, y, z 인자 값들을 넘깁니다. translate3d CSS 함수는 3D 공간에 요소의 위치를 이동시킵니다.
그리고 rotateX, Y, Z 메소드를 통해 회전을 시킵니다. 이 메소드들은 인자값으로 각도 또는 라디안을 줘야 되는데 deg(각도) 보단 rad 가 좀 더 사용하기 편하므로 rad를 사용할 것을 권장합니다.
그리고 각 Face 들의 위치를 잡기 위해 background-position 속성에 값을 줍니다. background-position은 배경 이미지의 위치를 정하는 속성입니다.
추가적으로 backface-curling(backface-visibility: hidden) 을 주어서 브라우저가 렌더링 작업을 두번 하지 않도록 해줍니다. 이를 통해 렌더링 속도를 두 배 올릴 수 있습니다.
이제 각 div 들을 Face로 setting 할 준비가 되었습니다. 일일이 각 div에게 Face에 대한 CSS 속성을 주는 대신 class를 이용하면 모든 과정을 자동화할 수 있습니다. 값만 주고 맡기면 일을 시행해주기 때문입니다.
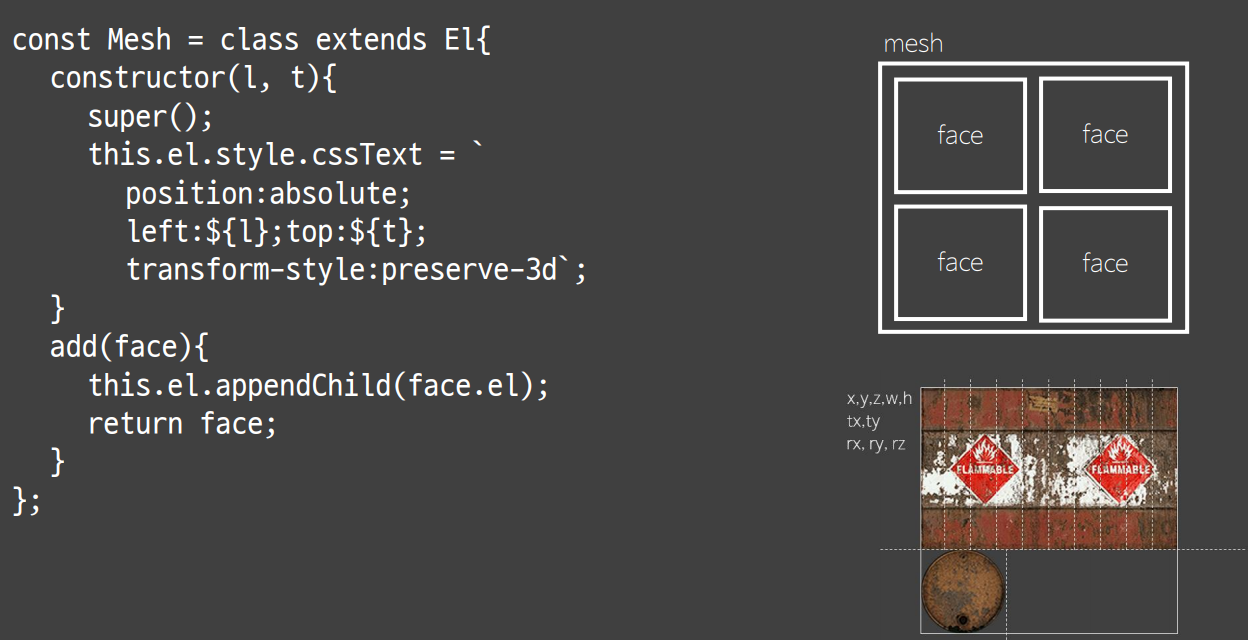
이제 Face들이 결집한 Mesh 클래스를 만들겠습니다. 마찬가지로 El 클래스를 상속받습니다. 그러면 우리 코드에선 자식 div 태그를 가진 div 태그가 mesh 인 것이죠. position:absolute 속성을 사용하므로 생성자의 인자로 left와 top을 줘서 위치를 지정합니다. 중요한 것은 transform-style:preserve-3d 속성을 준 것입니다. 이렇게 함으로써 DOM 구조상 자식들은 부모의 3D 속성을 물려받게 됩니다.
add 함수로 mesh 안의 자식으로 인자값인 face를 집어넣습니다.
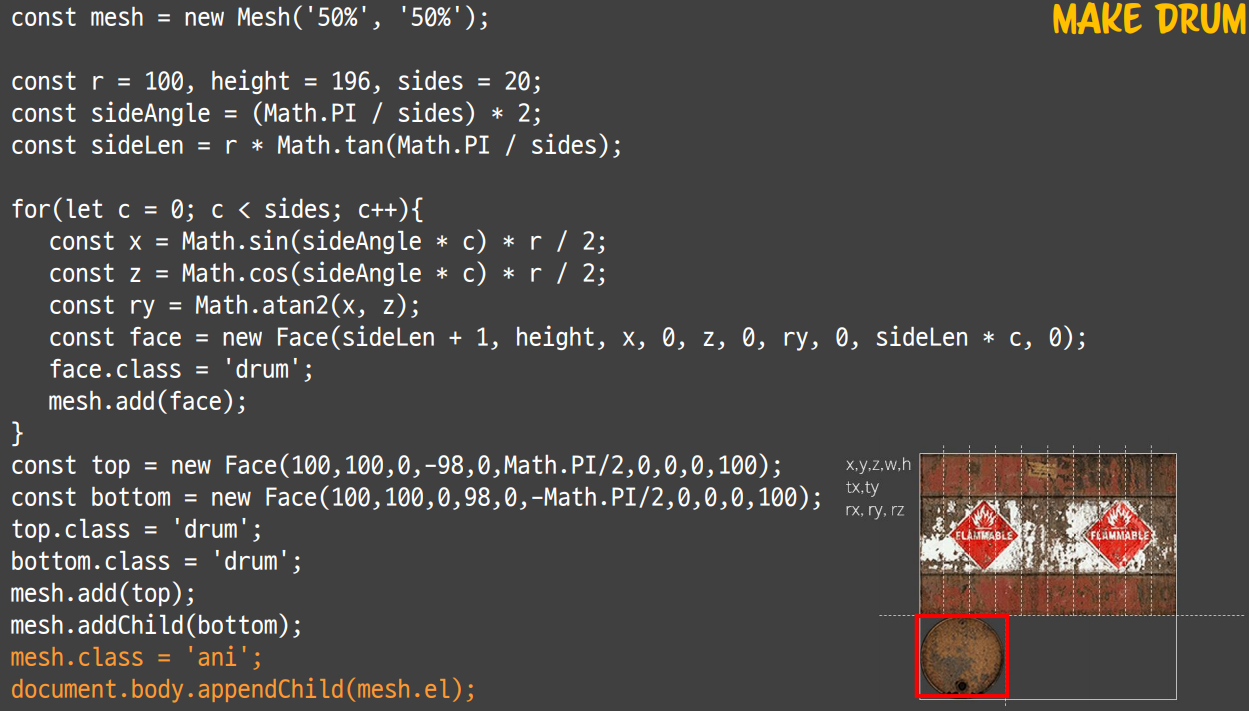
r은 지름 값이고 height는 원기둥의 높이 입니다. sides는 직사각형 Face들의 갯수입니다. 이 sides가 4개이면 사각형 형태를 갖추고 그 이상으로 늘어나면 점점 원의 형태를 가지게 됩니다.
sideAngle은 PI를 sides 만큼 나눈 값에 2를 곱하여 구합니다. 이 때 sideAngle은 중심점을 향한 각도를 의미합니다. 2를 곱하는 이유는 PI 라디언이 180도에 해당하기 때문입니다. 우리는 반원이 아니라 원 전체에 대한 각도를 구하고 있으므로 2를 곱하여 전체 원에 대한 각도를 구합니다.
PI 라디언이 180도에 해당하는 이유 :
sideLen은 빗변의 길이를 의미합니다. 이를 구할 때 sin또는 tan 중 선택하여 사용할 수 있는데 tan를 쓰면 부족함없이 꽉꽉 채워져서 그려지고 sin은 틈이 생깁니다 (실제로 tan 대신 sin을 쓰면 틈이 생깁니다. 그러나 현의 길이를 구하는 올바른 공식은 sin 인데 어떻게 tan로도 표현이 잘 되는지 잘 모르겠습니다 ㅠ 증명법을 모른다고 해야될까..)
지이사님의 설명에 따르면 다음과 같습니다. 원통은 다름 그림과 같이 다수의 face가 원통을 감싼 듯한 형태로 그려지며 이 면들이 무수히 많아지면 원통 모양으로 보이게 됩니다.

face 들이 여러개 합쳐졌을 때 그려지는 형태는 오른쪽입니다.
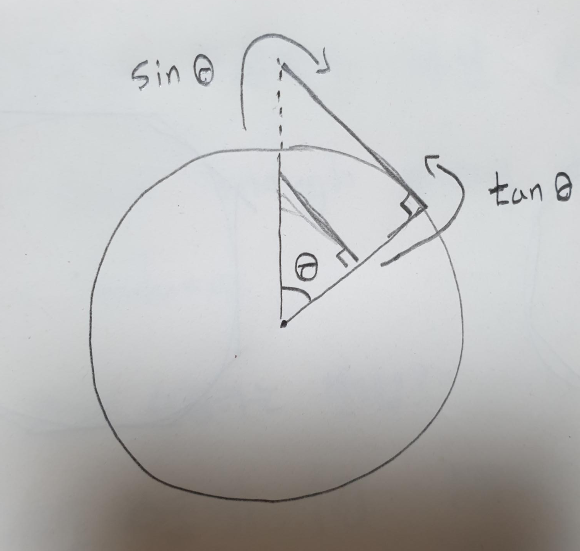
그래서 원통 바깥쪽으로 빗변이 그려질 때 같은 각도에 대해서 sin 보다 tan 이 더 큰 값으로 나타납니다. sin은 점선만큼 늘어난 길이가 분모 값으로 들어가면서 tan 보다 더 적은 값이 되기 때문입니다. 그러나 face의 수가 많이 늘어날수록 sin 과 tan 의 차이는 크게 없습니다.
이제 각 for 문을 돌면서 x,y,z,tx,ty,rx,ry,rz 값을 만들어 face 클래스에게 넘겨주겠습니다. 한가지 알아야 할 것은 x,z 좌표만 필요하고 y좌표는 필요없습니다. 우리는 바닥에 놓일 그림을 그릴 것이고 y는 위로 올라오는 값이므로 필요가 없습니다. 다음 사진을 보면 더욱 이해가 될 것입니다.
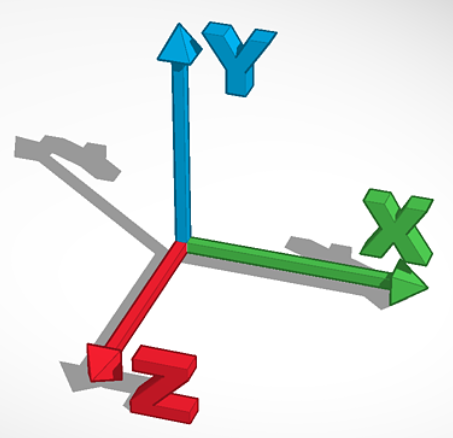
이 때 특정 각도에 위치한 점의 좌표를 구하고 싶은데 라디안을 알고 있다면 sin, cos 함수를 이용해서 x와 z 값을 구할 수 있습니다. sin은 x 좌표를 구할 때 쓰고 cos는 y 좌표를 구할 때 쓸 수 있습니다 (우리가 구하는 3d 세계에선 z좌표가 y좌표가 됩니다)
그리고 y축 으로만 회전할 것이므로 ry 값을 atan2 (아크탄젠트2, arctan2) 함수를 이용하여 구합니다. 이 때 왜 atan2 함수를 사용해서 구할까요?
결론적으로 말하면
- x, z 값을 알 때 수평축으로부터 각도를 구하려면 tan 함수를 써야 하고
- 각도 Θ 를 얻으려면 arc 류의 함수를 써야 함
- 원통은 360도를 가지는데 이 때 atan2 를 써야만 제 1,2,3,4 사분면에 대해서 처리를 해줄 수 있기 때문 (atan를 쓰면 제 1,2 사분면밖에 처리할 수 없음)
세번째 요인에 대해서 좀 더 이해를 할 필요가 있습니다.
arctan 의 범위와 arctan2 의 범위는 다음과 같습니다.
arctan 범위 : (-PI / 2, PI / 2)
arctan2 범위 : (-PI, PI]
다음 tan 그래프 그림을 보세요.
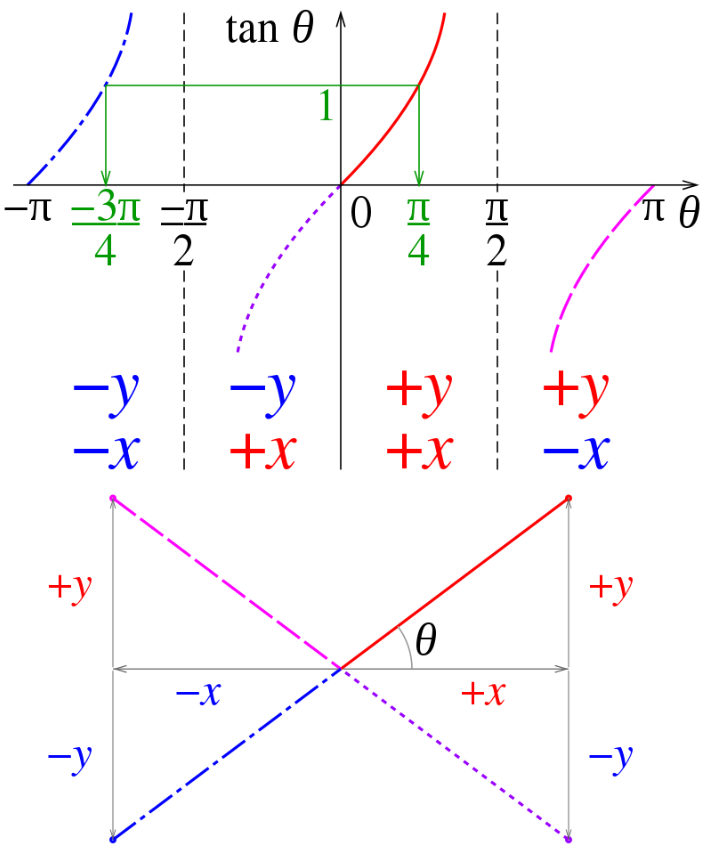
예를 들어, Θ 가 2사분면의 각이라고 하면 x = 1 이 아닌 x = -1 과의 교점으로 값을 구합니다. 그러면
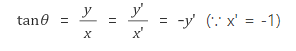
와 같이 되면서 tanΘ 의 부호가 - (마이너스) 입니다.
마찬가지로 Θ 가 4분면의 각이라면 x = -1 과의 교점으로 값을 구하므로 tanΘ 의 부호는 - (마이너스) 가 되며 두 사분면의 부호는 똑같이 나옵니다.
1사분면과 3사분면 일 때의 tanΘ 부호도 서로 똑같습니다.
결국 1, 3사분면의 tanΘ 부호가 동일하고 2, 4사분면의 tanΘ 부호 또한 동일하므로 Θ 가 어느 사분면에 속하는지 알 수 없습니다. 그러므로 tan의 역함수인 arctan 함수에서 좌표를 주어 각도를 구하면 1사분면 또는 2사분면에서의 각도만을 반환하는 한계가 있습니다.
이를 위해선 tan값으로만 판단하는 것이 아니라 sine 과 cosine 값을 각각 구별해서 볼 필요가 있는데, 이 작업을 arctan2 함수가 합니다.

sin과 cos 함수로 arctan 값을 구하고 그 arctan 결과 값에 PI를 더하여 모든 사분면에 해당하는 각도를 구할 수 있습니다.
그래서 arctan2 함수는 tan 그래프 사진에서처럼 x,y 값이 다를 때 -3PI/4, PI/4 와 같이 구분되는 arctan 값을 반환하므로 정확한 각도를 구할 수 있습니다.
이제 구한 값들을 face 클래스의 인자로 넘겨주고(sideLen에 1을 더한 것은 틈이 벌어지지 말라고 넣어준 것이라고 설명하심) class 이름 지정과 face 를 mesh 에 add 하여 하나의 작업을 마무리합니다.
여기까지가 직사각형 face를 구한 과정이었고 위 아래 원뚜껑 face에 대한 클래스 또한 좌표들을 대입하여 만듭니다. 이 때 윗 원뚜껑은 y좌표가 -98이고 아래 원뚜껑은 98 입니다. 이들도 마저 mesh 클래스에 add 하여 작업을 마무리 합니다.
코드를 돌려보면 드럼통이 막 회전하는 모습을 확인할 수 있습니다.
지금까지 3D 관련한 기본 개념들을 배우고 이를 Javascript 코드로 짜서 3D 입체 그림을 직접 표현해보았는데요,
Javascript 로만 이러한 3D 그림을 그릴 수 있을까요? 아닙니다. CSS + HTML 만 사용해도 할 수 있습니다. 그 중 SASS 라는 CSS 언어와 SASS의 라이브러리인 COMPASS 를 이용하여 구현해보겠습니다.
SASS + COMPASS
SASS는 기타 다른 프로그래밍 언어처럼 사용할 수 있습니다. 함수 선언이 가능하고, 또 함수의 반환값 또한 사용할 수 있습니다. 또 컴파일러 기능 또한 존재하여 사용자가 코드를 작성하면 CSS 파일을 만들어냅니다.
SASS는 프로그래밍적인 특징을 갖는데 하나씩 살펴보겠습니다.
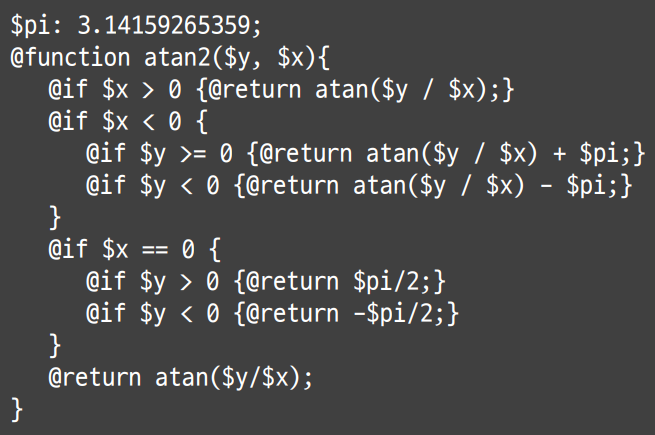
우선 변수를 선언하고 사용할 때 달러 표시($) 를 변수명 앞에 붙이고, 콜론(:)으로 변수를 삽입합니다. 다른 언어처럼 = 를 사용하지 않는데 부등호와 헷갈리기 때문에 사용하지 않습니다.
그리고 다른 언어와 마찬가지로 예약어 개념이 존재하는데 function, return, for 와 같은 예약어를 쓸 때 앞에 골뱅이 문자(@)를 붙입니다. 다른 언어와 차별되는 장점 중 하나로 이렇게 예약어를 쓸 때 @를 써줘야지 작동되므로 초보자들이 겪는, '어떤 게 예약어 인지 분간이 안돼?' 와 같은 문제를 줄일 수 있습니다.
또 문자열 처럼 사용하고 싶을 때 샾(#) 중괄호를 사용하면 됩니다. => #{$w}px;
여기서 SASS 언어 자체에서는 atan 라는 함수를 제공하지 않으므로 compass 라이브러리에 가져다 써야합니다.
또 SASS에는 두 가지 종류의 함수가 존재합니다. 먼저 function이 있고 mixin 이 있습니다. function은 js에서 쓰듯이 선언하여 사용하면 되고 function 앞에 @만 붙여주면 됩니다.
function은 값 하나만 return이 됩니다.
mixin은 여러 개의 CSS 속성을 세트로 반환해줄 때 사용합니다. 선언하는 것은 function과 비슷합니다. 단 mixin을 사용할 땐 @include 키워드를 붙여서 사용합니다.
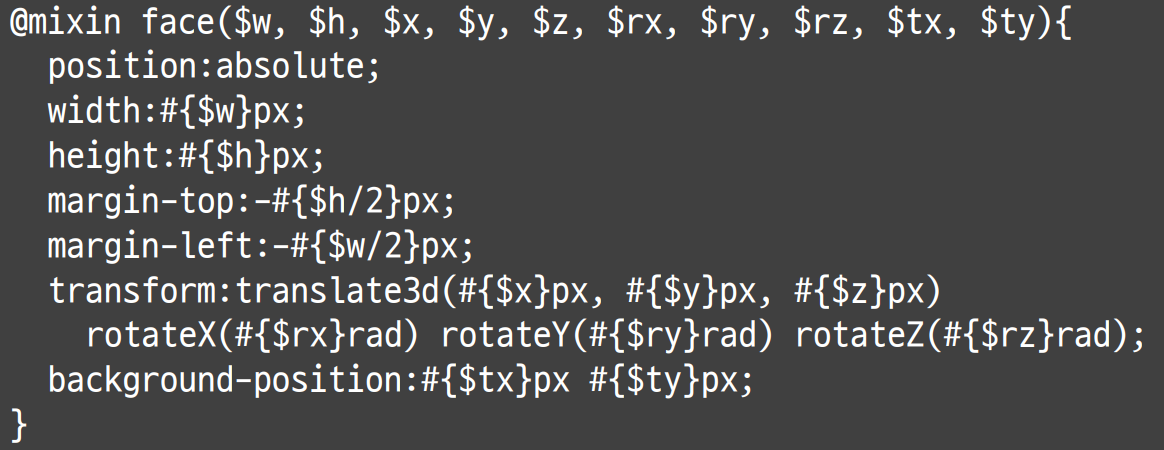
사용할 땐 => @include face(....)
for문 또한 우리가 알 던 for문과 거의 유사합니다.
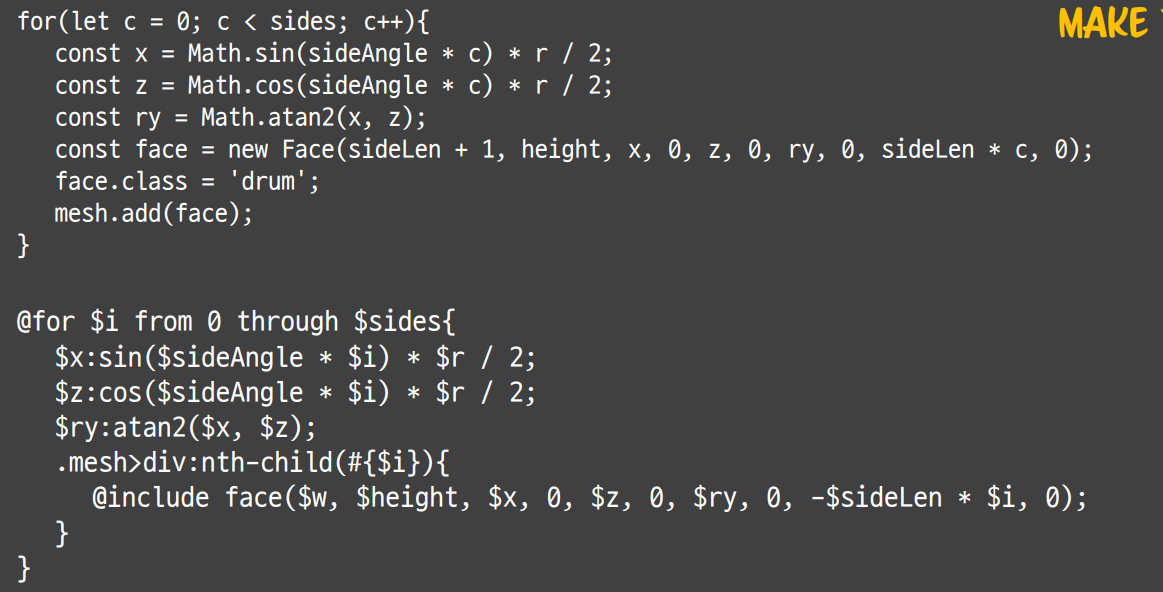
위의 코드가 js에서 짠 코드이고 아래의 코드가 SASS에서 사용하는 코드입니다.
from ~ through 구문을 사용하는 것이 특징입니다.
기존 코드의 흐름대로 그대로 짭니다. mesh 속성을 가진 div 태그 내에 nth-child로 꽂아넣는 것 또한 appendChild 메소드로 자식 element로 붙여넣는 행위와 유사합니다.
그냥 CSS만 사용했을 때와 SASS로 작업했을 때 이점은 SASS는 컴파일이라는 과정을 가지고 있어서 사람이 일일이 세부적인 부분을 건들일 필요가 없이 컴파일러가 알아서 다 처리해준다는 것입니다. 예를 들어 위에서 각 face마다 y축으로 회전하는 값인 ry가 각각 다른데 컴파일러가 이 값을 알아서 처리해줍니다. 사람이 일일이 값을 입력할 필요가 없습니다.
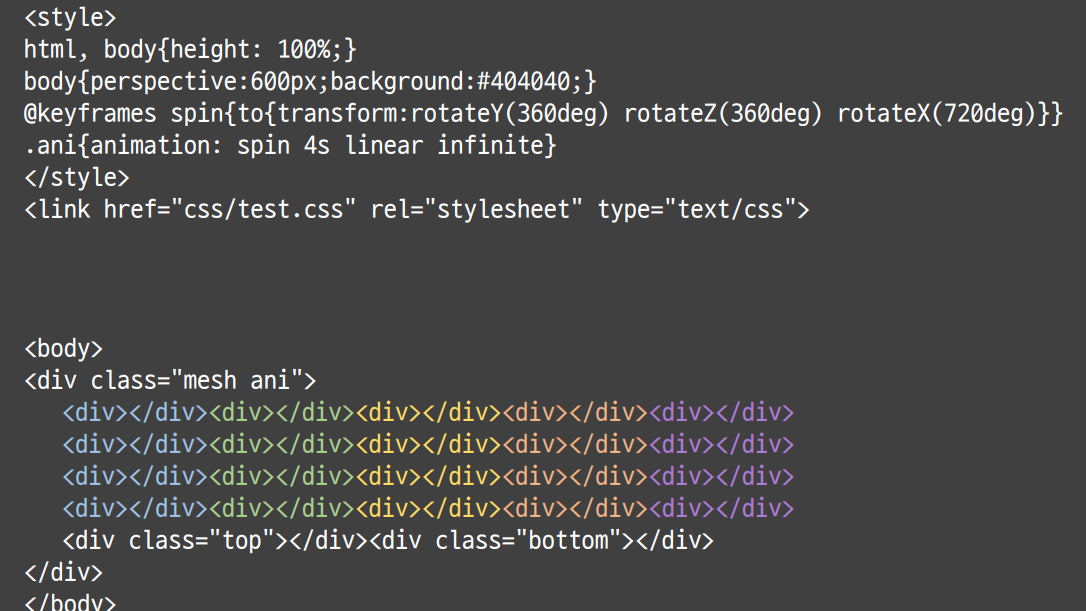
이제 마지막으로 html에 기본 틀을 잡아줍니다.
sides를 20개 만들었으니 div 태그 또한 20개 만들어줍니다. 만약 sides를 4개로 지정해주고 싶다면 SASS에서 $sides 변수값만 변경해주면 됩니다 (이 경우 속성이 적용된 4개 div외에 나머지 div는 html에 찍히더라도 드럼통 그림에는 전혀 영향을 미치지 않습니다)
CSS Sprite 추가자료 :
http://tcpschool.com/css/css_basic_imageSprites
translate3d 추가 자료 : https://developer.mozilla.org/ko/docs/Web/CSS/transform-function/translate3d
background-position 추가 자료 : https://www.codingfactory.net/10595
원주율과 라디안 사이의 관계 : https://m.blog.naver.com/PostView.nhn?blogId=wyepark&logNo=220517029219&proxyReferer=https%3A%2F%2Fwww.google.com%2F
현의 길이 구하는 방법 : https://kin.naver.com/qna/detail.nhn?d1id=11&dirId=110403&docId=115029847&qb=7ZiE7J2YIOq4uOydtCDspp3rqoU=&enc=utf8§ion=kin&rank=3&search_sort=0&spq=0
아크탄젠트2 : https://en.wikipedia.org/wiki/Atan2
atan와 atan2 차이 : https://stackoverflow.com/questions/283406/what-is-the-difference-between-atan-and-atan2-in-c
'FrontEnd > CSS 관련자료' 카테고리의 다른 글
| vertical-align 속성으로 이미지 공백 지우기 (1) | 2020.01.21 |
|---|---|
| 모던 웹 디자인의 정석(1장) (0) | 2019.11.10 |
| 코드스피츠 76-3 (CSSOM & Vendor Prefix)-2 (0) | 2019.10.31 |
| 코드스피츠 76-3 (CSSOM & Vendor Prefix) (0) | 2019.10.20 |
| 코드스피츠 76-2 (Box model & Absolute Position) (0) | 2019.10.08 |




댓글