개요
동적 계획법을 공부한 내용을 정리하기 위해 작성하였습니다. 공부하신 분들께 도움이 되면 좋겠습니다.
개념
정의 : 두 번 이상 반복 계산되는 부분 문제들의 답을 미리 저장함으로써 속도의 향상을 꾀하는 알고리즘 설계 기법
큰 의미에서 보면 분할 정복과 같은 접근 방식을 의미합니다. 처음 주어진 문제를 더 작은 문제들로 나눈 뒤 각 조각의 답을 계산하고, 이 답들로부터 원래 문제에 대한 답을 계산해냅니다. 동적 계획법은 답을 여러 번 계산하지 않고 한 번만 계산하는데 이 계산 결과를 재활용함으로써 속도 향상을 꾀할 수 있습니다. 여기서 답을 메모리에 저장하는데 이 메모리의 장소를 캐시(cache)라고 부릅니다.
메모이제이션
앞서 캐시를 이용한 것처럼 결과를 저장하는 장소를 마련해두고, 한 번 계산한 값을 저장해 뒀다 재활용하는 최적화 기법을 메모이제이션(memoization)이라고 부릅니다.
메모이제이션을 적용할 수 있는 경우
입력이 같을 때 항상 같은 결과를 반환하는 경우에만 적용가능 합니다. 이처럼 함수의 반환 값이 그 입력 값만으로 결정되는지 여부를 참조적 투명성(referntial transparency)이라고 합니다.
메모이제이션 구현 패턴 (C/C++ 언어 기준으로 설명합니다)
- 항상 기저 사례를 제일 먼저 처리합니다.
- 입력이 범위를 벗어난 경우 등을 기저 사례로 처리하면 매우 유용한데, 기저 사례를 먼저 확인하지 않고 cache[]에 접근하면 범위를 벗어나는 등의 오류가 있을 수 있거든요
- 함수의 반환 값이 항상 0 이상이라는 점을 이용해 cache[]를 모두 -1로 초기화했습니다.
- cache[]의 해당 위치에 적혀 있는 값이 -1이라면 이 값은 계산된 반환 값이 아니라고 할 수 있습니다. 그러나 만약 함수의 반환 값이 음수일 수도 있다면 다른 값으로 초기화를 해야합니다.
- ret가 cache[a][b]에 대한 참조형(reference)이라는 데 유의하세요.
- 참조형 ret의 값을 바꾸면 cache[a][b]의 값도 변하기 때문에 답을 저장할 때도 매번 귀찮게 cache[a][b]라고 쓸 필요가 없어집니다. 이 트릭은 특히 cache가 다차원 배열일 때 유용합니다. 인덱스 순서를 바꿔 쓰는 등의 실수를 줄여줍니다.
메모이제이션의 시간 복잡도 분석
(존재하는 부분 문제의 수) * (한 부분 문제를 풀 때 필요한 반복문의 수행 횟수)
동적 계획법 풀이순서
- 주어진 문제를 완전 탐색을 이용해 해결한다
- 중복된 부분 문제를 한 번만 계산하도록 메모이제이션을 적용한다
예제
Leetcode 46. 와일드카드 매칭
주어진 문자열이 해당 패턴을 통과하는지 여부를 boolean 값으로 출력하기.
풀이
* (와일드카드) 패턴에 대한 처리가 까다롭다. he*p 와 help에 대한 매칭은 쉽지만 *bb* 와 babbbc 처럼 * (와일드카드)의 범위가 명확하지 않은 경우 문자열 어디까지 대응되는지 알아내야 한다. 또한 메모이제이션을 사용하기 위해 배열의 크기를 얼만큼 한정해야 하는지도 변수다.
동적 계획법 풀이법에 따라 완전 탐색 방식으로 먼저 풀면 아래와 같다.

첫번 째 while 문은 더 이상 패턴과 일치하는 문자가 없을 때 종료되며 구체적인 종료 조건은 아래와 같다.
- s[pos]와 w[pos]가 대응되지 않는다
- w 끝에 도달했다 : 패턴에 * 가 없는 경우가 해당되며 패턴과 문자열의 길이가 같아야만 정답이라고 볼 수 있다
- s 끝에 도달했다 : 패턴은 남았지만 문자열이 이미 끝난 경우. 만약 남은 패턴이 전부 * 라면 정답이 될 수 있다
- w[pos]가 * 인 경우 : * 에 문자열이 몇 글자나 대응될지 모르므로 코드에서 보이는 for 루프로 0 글자부터 문자열 끝까지 순회하면서 검사한다.
만약 match(w.substr(pos+1), s.substr(pos+skip))으로 재귀 호출하여 답이 하나라도 참이면 정답이 될 수 있다.
제대로 이해하기-1
위에서 언급한 조건 중 4번째 조건이 잘 이해안되었다.
- w.substr(pos + 1) 을 넘기는 이유
- * 는 모든 문자열에 매칭된다. 그러므로 * 다음에 있는 패턴과 문자열을 비교해 * 패턴이 어디까지 매칭되는지를 확인한다.
- 만약 a** 과 같이 * 다음에 또 * 이면?
- 우리가 알고 있는 바로는 앞에 'a'가 붙는 문자열이면 무엇이든 일치한다.
- 코드상으로는 어떻게 동작하는지가 궁금해서 확인해보니 아래와 같다.
- 디버깅을 통해 확인한 결과 마지막 * 패턴이 수행하는 재귀호출에서 하단의 for 루프를 돈다. 이 때 남은 패턴은 empty string("")이다.
- for 루프에서 "" 패턴과 문자열을 비교할 때 마지막 단계에서 문자열도 "" 이 되어 서로 일치하게 된다. 그래서 true를 반환된다.
- 결론 : w.substr(pos + 1) 을 넘겨주는 게 맞다!
- s.substr(pos + skip) 을 넘기는 이유
- 이전 while 문( * 패턴이 나오기 전까지) 에서 패턴과 문자열이 어디까지 일치하는지를 pos 값을 증가시키면서 확인했으므로
- 이 후 * 패턴과 문자열이 어디까지 일치하는지 한 글자씩 확인해야 한다.
- 문자열과 패턴이 서로 일치할 때까지 for 루프내에서 skip 변수 값을 증가시키며 재귀호출을 한다.
- 결론 : s.substr(pos + skip)을 넘겨주는 게 맞다!
- 답이 하나라도 참이면 정답이 될 수 있다?
- * 패턴은 어떤 문자열과도 매칭이 된다. 0개 이상 붙어도 정답이 된다. (즉 매칭되는 게 없어도 정답이다)
- ex) a* : a, ab, abc, aabbc ..., he*p : hep, help, hellop, hellp...
- 그렇기 때문에 하나라도 참 값을 반환하면 정답이 되게끔 만든 것이다.
- 정리 : 결국 * 패턴이 쓰이면 어떤 문자열이라도 매칭이 되므로 무조건 정답이 된다고 보는데 그러므로 재귀호출을 하면서 하나 이상의 참인 값을 찾는 것임.
- 결론 : 하나라도 참인 값이 나오면 정답이다!
( 책의 설명이 완전 초급자를 위한 설명이 아니므로 헷갈릴 수도 있습니다. 저 같은 경우 디버깅을 여러번 하면서 저자의 표현을 어느정도 이해할 수 있었습니다. 코드를 직접 짜서 디버깅을 해보면 천천히 이해되실 수 있을 것입니다 )
중복되는 부분 문제
그러나 이렇게 풀 경우 **********a 와 aaaaaaaaaaaaaab 같은 케이스에 대해서 오랜 시간이 걸릴 수 있다. 왜냐하면 각 패턴과 문자열의 끝에 닿을 때까지 검사를 멈추지 않을 것이기 때문. 이 때 코드를 실행하면서 수행하는 계산에 중복이 발생하고 있다면 이를 메모리에 저장하여 사용하는 메모이제이션을 적용하여 수행 시간을 줄일 수 있다.
배열의 크기는 최대 크기 + 1 로 잡고 초기화 한다. ( 코드 상에서 w + 1 또는 s + 1 과 같이 처리하는 부분이 있어 만약 딱 최대 입력 크기로만 선언하면 OutofRange 오류가 발생할 수 있다. 그러므로 최대 입력 크기 + 1 만큼의 사이즈로 설정하자)
전체 시간 복잡도 = (부분 문제의 개수= n^2) * (for 루프 최대 반복 횟수 n) = O(n^3)
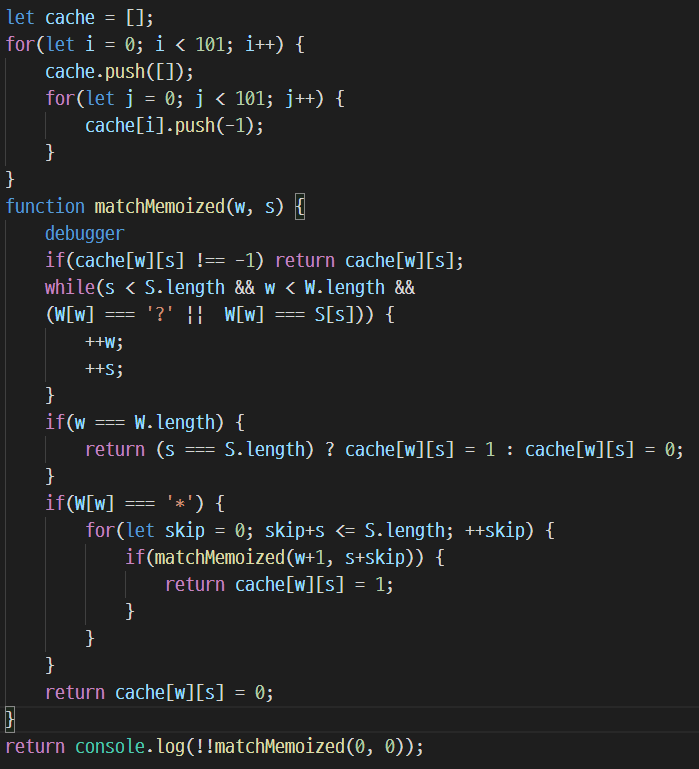
패턴과 문자열이 얼만큼 일치하는지 확인하는 인덱스 값 pos 대신 w,s 가 들어갔지만 앞의 코드와 거의 비슷하다. (w, s 를 쓴 것은 이 후 for 루프를 재귀 호출로 바꿀 때 사용하기 위함이다)
for 반복문의 범위는 s+skip으로 계산하는데 w+skip 으로 해도 똑같이 동작한다. 다만 * 패턴에 문자열의 어디까지가 대응되는지를 확인하는 것이므로 s+skip이 의미상으로 더 적합하다.
다른 분해 방법
이 때 코드의 반복문을 재귀 호출로 바꿔주면 O(n^2)으로 풀 수 있다. 먼저 while 문을 보자.
while 문 조건을 통과했다는 것은 패턴과 문자열이 서로 일치한다는 것이다. 이 때 w와 s를 1씩 증가하는 대신 바로 다음에 있는 문자와 패턴을 재귀 호출 인자로 보내서 서로 대응되는지 확인할 수 있다. 그러면 아래와 같이 바뀐다.

이제 남은 것은 for 루프인데, for 루프를 재귀 호출로 바꾸는 것은 처음에는 익숙치 않다. 책에서 설명하는 포인트는 크게 2가지인데,
- 매 단계에서 *에 아무 글자도 대응시키지 않을 것인지 (0 글자에 대응되는 경우)
- 한 글자를 더 대응시킬 것인지 (한 글자에 대응되는 경우)
를 결정하면 된다.
그러면 다음과 같이 바뀔 수 있다.

matchMemoized(w+1, s) 는 루프 첫 단계와 대응되며 만약 * 패턴이 처음 등장하면 해당 재귀 호출로 처리된다.
(이해가 안되는 건 matchMemoized(w, s+1) 부분인데, 왜 w+1 이 아닌 w 로 넘겨주는 지 이해가 안되었다. 재귀 호출을 적용하기 전의 코드에선 *가 어디까지 대응되는지 알기 위해 바로 다음 자리의 인덱스 w+1 를 인자로 넘겨 for 반복문을 돌리지 않았는가? 여기선 왜 갑자기 w 만을 인자로 넘기는지 이해가 안된다.. 디버깅을 돌려보니 w+1 대신 w를 인자로 넘겼을 때 캐시 배열이 더욱 꼼꼼하게 채워지는 것을 확인했다. 이를 통해 메모이제이션을 활용할 수 있는 가능성이 높아지고 결과적으로 속도 향상이 이뤄지게 된다고 판단하였다)
재귀 호출을 적용한 전체 코드는 아래와 같다.

이제 책의 코드를 Leetcode 문제에 맞게 입출력 값을 알맞게 바꿔주면 된다.
유의사항
Leetcode 문제의 경우 패턴 및 문자열의 최대 크기를 따로 명시하지 않았기 때문에 캐시 배열을 초기화 때 사용자가 적당히 크기를 설정해줘야 한다. (본인의 경우 문자열/패턴의 길이 + 100 로 배열 크기를 초기화하였음)
작성 코드

나머진 입력으로 문자열과 패턴을 받고 만든 정답 함수의 시작을 첫 부분(0, 0) 에서 시작한 것 뿐, 로직은 동일하다.
출처
알고리즘 문제 해결 전략 (구종만 저)
'Algorithm 개념 및 문제풀이 > Knowledge' 카테고리의 다른 글
| 연결리스트(Linked-list) 개념 정리 및 문제 풀이 (0) | 2020.02.18 |
|---|

댓글