개요
Leetcode 에서 알고리즘 문제를 풀고 배운 내용을 정리하기 위해 작성하였습니다.
문제 : 4. Median of Two Sorted Arrays
주어진 두 배열들에서 중간값(Median)을 구해야 함.
** 중간값은 말 그대로 배열의 중간에 위치한 값임. 이 때 배열요소의 갯수가 홀수이면 중간에 있는 요소가 정답이 되지만 짝수이면 중간위치 주변의 값들의 평균이 정답이 됨.
풀이1 : Bruce force
주어진 두 배열을 합친 후, 합쳐진 배열에서 중간값을 찾음.
이 때의 시간복잡도는 O(m + n) 이며 공간복잡도 또한 O(m + n) 으로 동일함.
풀이2 : Binary Search
Binary Search 로 풀기 위한 방법에는 배열을 적당히 나누는 기법이 들어가는데, 이에 대한 이해가 문제풀이의 핵심이므로 꼭 알아야 함.
두 배열의 총 요소 개수 : 짝수
다음과 같이 두 배열이 주어져 있다고 하자.

X, Y 배열은 각각 오름차순으로 정렬되어 있는 배열들이고 두 배열의 요소를 총 합하면 14개로 짝수개가 나온다.
그리고 두 배열을 각각 적당한 크기로 나눈다.

나눴을 때 배열 요소의 개수가 일치해야 한다. 위 그림처럼 빨간박스를 씌운 요소들과 파란박스 요소들 개수가 서로 똑같이 나오도록 나눠야 한다. 현재 7개씩 나누어졌다.
각각 오름차순으로 나열된 배열들이고, x2 와 y5는 자신의 좌측 요소들 중 가장 큰 요소들이다.
이 때 다음과 같은 가정을 한다.

만약 위와 같다면 빨간 박스 요소들은 파란 박스 요소들보다 무조건 작거나 같다.
그렇다면 중간값은 x2, y6, y5, x3 를 이용하여 구할 수 있으며 중간값은 다음 연산의 결과가 된다.

즉 x2, y5 중 최대값과 x3, y6 중 최소값의 평균값이 중간값이 된다.
이 부분을 좀 더 이해하자면 다음을 보자.

배열 요소가 크기 순으로 차례되어 정렬되어있다. 이 때 빨간 박스 요소들은 파란 박스보다 무조건 작다. 그러면 중간값은 어떻게 구하는가? 위 그림에서 중간값은 z4 와 z5의 평균값이다. z4는 빨간 박스의 최대값이고 z5는 파란 박스의 최소 값이다. 이들의 평균으로 중간값을 구하는 것이다. 위 연산은 이러한 개념을 이용한 것이다.
두 배열의 총 요소 개수 : 홀수
홀수는 간단하다. 아까 살펴 본 배열들에서 요소 하나가 추가된 상태라고 보자.

마찬가지로 큰 값과 작은 값들로 나눈 상태이다. 이 때 빨간 박스의 크기, 즉 작은 값들 집합의 총 요소 수는 파란 박스(큰 값들의 집합) 보다 하나 더 크다. 위에서 했던 가정(x3 <= y6, y5 <= x4)이 맞다면 이 때 중간값은 빨간 박스에서 가장 큰 값이 된다.
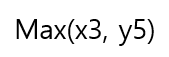
Binary Search 풀이
위 개념을 토대로 코드를 작성하기 전에 빨간 박스와 파란 박스로 나누어 경계값 포인트(아까 봤던 x2-x3, y5-y6) 를 구하는 과정이 필요하다.
이를 Binary Search를 사용하여 구할 것이며 이렇게 해서 답을 구했을 때 시간복잡도는 O(log (min(x, y) ) 가 나온다. x, y는 각 배열의 길이를 의미한다. 실제 배열을 갖고 살펴보자.
두 배열의 총 요소 개수 : 홀수
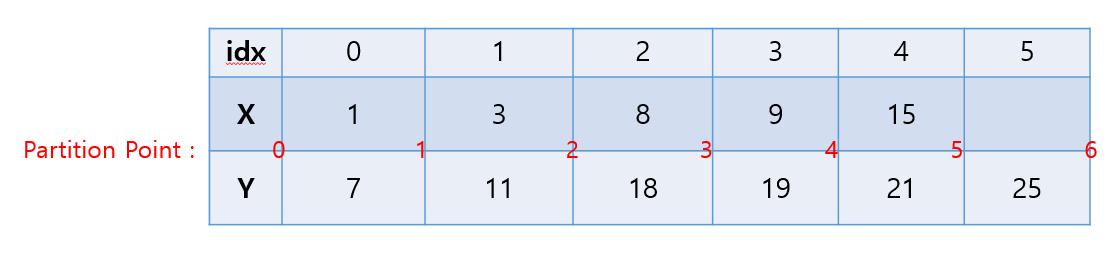
위 그림과 같은 두 배열이 있다고 하자.
우선 두 배열을 합쳐서 나열하면 [1, 3, 7, 8, 9, 11, 15, 18, 19, 21, 25] 가 나오며 중간값은 11이다. 이 값을 Binary Search를 통해 구할 것이다.
Binary Search를 할 때 4가지 변수와 한 가지 간단한 공식에 대해서 유념해야 한다.
- start : Binary Search(BS)를 시작할 인덱스.
- end : BS를 끝낼 인덱스.
- partition X : X 배열의 현재 partition point. (start + end) / 2 로 값을 구함.
- partition Y : Y 배열의 현재 partition point. 아래 공식을 통해 값을 구함.


partition point 라는 것이 있는데, 이는 큰 요소와 작은 요소를 나누는 기준점을 의미한다. partition X, Y는 이 값을 갖는데 예를 들어 partition X = 2, partition Y = 3 이라면 X, Y 배열은 각각 다음과 같이 나뉜다.
X = [1, 3] | [8, 9, 15]
Y = [7, 11, 18] | [19, 21, 25]
그리고 partition Y의 값을 구할 때는 위의 공식을 이용한다. 즉
partition Y = (X + Y + 1) / 2 - partition X 를 통하여 값을 구한다.
X, Y 에 +1 을 하는 것은 배열의 총 갯수가 홀수이거나 짝수 일때 두 경우의 연산 모두 잘 수행(play well)하기 위해서다.
그리고 partition point를 정했을 때 우리가 정한 가정이 맞는지 확인을 한다. 만약 잘 들어맞지 않았을 때는 start 또는 end 인덱스를 왼쪽 이나 오른쪽 으로 한칸씩 옮긴다.
그래서 partition X를 가지는 X 배열은 연산의 기준이 되는데, 이 X 배열을 정할 때는 두 배열이 주어져 있을 때 다른 배열보다 상대적으로 작은 크기를 갖는 배열을 X 배열로 지정하면 된다.
변수와 공식에 대한 설명이 끝났으니 이제 실제로 예제를 파보자.
첫번째 단계

start 는 처음부터 시작하므로 0이고 end는 partition(분해)가능한 끝지점을 의미하므로 5가 된다.
즉 우리는 x 배열에 대해서 partition point = 0을 하여 왼쪽의 요소는 0개, 오른쪽에는 5개 둘 수 있고
partition point = 0을 하여 왼쪽의 요소는 0개, 오른쪽에는 5개 둘 수 있고
partition point = 1을 하여 왼쪽의 요소는 1개, 오른쪽에는 4개 둘 수 있고
partition point = 2을 하여 왼쪽의 요소는 2개, 오른쪽에는 3개 둘 수 있고
partition point = 3을 하여 왼쪽의 요소는 3개, 오른쪽에는 2개 둘 수 있고
partition point = 4을 하여 왼쪽의 요소는 4개, 오른쪽에는 1개 둘 수 있고
partition point = 5을 하여 왼쪽의 요소는 5개, 오른쪽에는 0개 둘 수 있기에 총 6번의 partition이 가능하다. 이렇기 때문에 end는 5가 되는 것이 맞다.
이렇게 start, end를 구했으므로 이들의 평균값을 partition X에 대입한다. 만약 소수점 값이 나온다면 정수만을 취한다.
그리고 partition Y를 구하는 공식에 대입하여 partition Y 값까지 구한다.
그러면 배열은 다음과 같이 나눠진다.

형형색색한게 눈이 아프지만 같이 잘 살펴보자
X 배열의 좌측은 [1, 3] , 우측은 [8, 9, 15] 가 되고
Y 배열의 좌측은 [7, 11, 18, 19] , 우측은 [21, 25] 가 된다. 이제 우리가 세운 가정으로 비교를 해보자.
X배열 좌측의 최대값은 3 이고 Y 배열 우측의 최소값은 21 이다. 3은 21보다 작으므로 맞다.
Y배열 좌측의 최대값은 19 이고 X 배열 우측의 최소값은 8 이다. 19는 8보다 작지 않으므로 틀리다.
이 경우 우리가 X 배열에서 partition point를 너무 좌측에 둔 것이므로 이를 우측으로 이동시켜줘야 한다.
그러므로 partition X에 1 더한 값을 start 에 넣어주고 다시 검색을 시작한다.

start는 partition X에 +1 한 값이므로 3이 된다. 우리는 기존 배열 검색 구간을 우측으로 이동시키는 것이므로 end에는 변화가 없다. partition X는 start, end의 평균값으로 구하고 partition Y는 partition X 값을 토대로 구한다.
이제 구한 partition point를 토대로 배열을 나누면 다음과 같다.
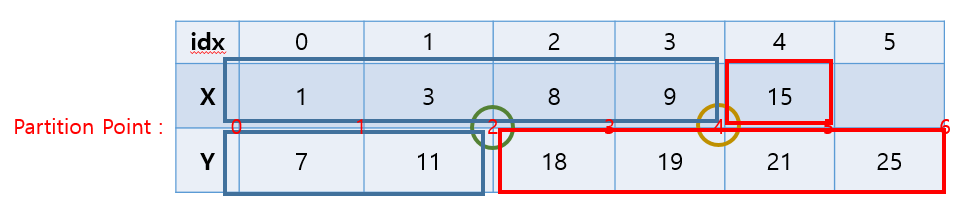
X 배열의 좌측은 [1, 3, 8, 9] , 우측은 [15] 가 되고
Y 배열의 좌측은 [7, 11] , 우측은 [18, 19, 21, 25] 가 된다. 우리가 세운 가정으로 비교를 해보자.
X배열 좌측의 최대값은 9 이고 Y 배열 우측의 최소값은 18 이다. 9는 18보다 작으므로 맞다.
Y배열 좌측의 최대값은 11 이고 X 배열 우측의 최소값은 15 이다. 11은 15보다 작으므로 맞다.
이제 올바르게 배열을 나눴으므로 중간값을 구할 수 있다.
앞서 얘기한 것처럼 홀수의 경우 작은 값들 집합의 최대값이 된다. 이 경우 최대값은 11이 되므로 중간값은 11이 된다.
두 배열의 총 요소 개수 : 짝수
이제 배열의 총 요소 개수가 짝수일 때를 살펴보자. 이 때 처리가 까다로운 Edge case 로 예제를 볼 것이다.

두 배열을 합치면 총 10개이며 두 배열을 합치면 [3, 5, 7, 9, 11, 16, 23, 26, 31, 35] 순으로 정렬이 된다. 이 때의 중간값은 11과 16의 평균값인 13.5가 된다. 이를 Binary Search 를 이용하여 구해보자.
먼저 각 변수들 값부터 구한다.

end는 X 배열을 총 4번 나눌 수 있으므로 4가 된다. 그렇다고 end 값이 횟수 그 자체를 의미한다기 보단 partition 을 4번 만큼 가능하게 하는 인덱스를 의미한다고 보면 됨.
이제 partition X, Y를 기준으로 작은 값, 큰 값 집합으로 나누면 다음과 같이 나온다.

X 배열의 좌측은 [23, 26] , 우측은 [31, 35] 가 되고
Y 배열의 좌측은 [3, 5, 7] , 우측은 [9, 11, 16] 가 된다. 우리가 세운 가정으로 비교를 해보자.
X배열 좌측의 최대값은 26 이고 Y 배열 우측의 최소값은 9 이다. 26는 9보다 작지 않으므로 틀리다.
Y배열 좌측의 최대값은 7 이고 X 배열 우측의 최소값은 31 이다. 7은 31보다 작으므로 맞다.
이 경우 우리가 X 배열에서 partition point를 너무 우측에 둔 것이므로 이를 좌측으로 이동시켜줘야 한다.
partition X에서 -1 한 값을 end 값에 대입해주어 좌측 구간으로 이동하도록 한다. 그리고 각 변수의 값을 다시 구한다.
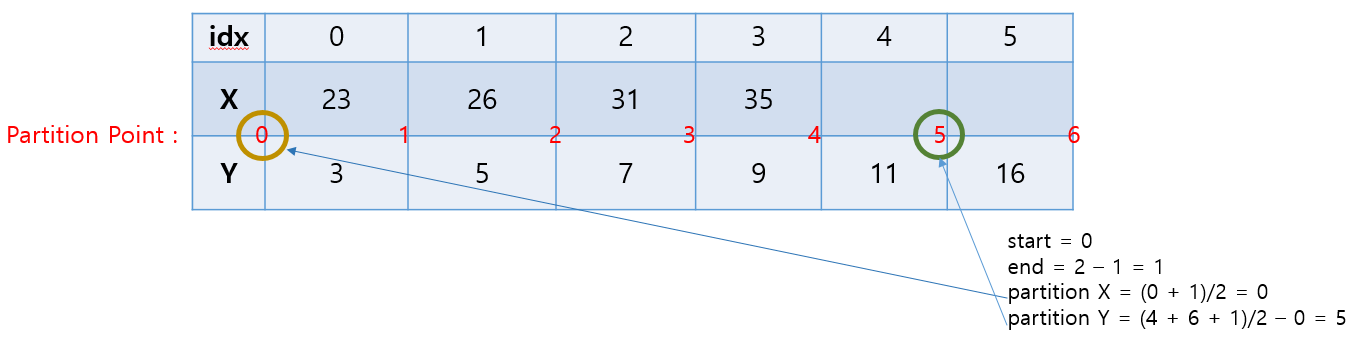
이제 구한 partition X, Y를 기준으로 작은 값, 큰 값 집합으로 나누면 다음과 같이 나온다.

X 배열의 좌측은 [] , 우측은 [23, 26, 31, 35] 가 되고
Y 배열의 좌측은 [3, 5, 7, 9, 11] , 우측은 [16] 가 된다.
예제가 edge case 인 이유가 위의 그림에 있다. X 배열의 좌측은 0 point 기준으로 나누어 빈 집합이 되버린다. 이렇게 빈 집합이 될 경우, 무한대 값을 하나 임의로 넣어준다.
만약 좌측 배열이 비었을 땐 -Infinity, 우측 배열이 비었을 땐 +Infinity 를 넣어준다.
이제 우리가 세운 가정으로 비교를 해보자.
X배열 좌측의 최대값은 -Infinity 이고 Y 배열 우측의 최소값은 16 이다. -Infinity는 16보다 작으므로 맞다.
Y배열 좌측의 최대값은 11 이고 X 배열 우측의 최소값은 23 이다. 11은 23보다 작으므로 맞다.
이제 올바르게 배열을 나눴으므로 중간값을 구할 수 있다.
짝수의 경우 작은 값들 집합의 최대값과 큰 값들 집합의 최소값의 평균이 중간값이 된다.
그래서 ( Max(-Infinity, 11) + Min(23, 16) ) / 2 = (11 + 16) / 2 = 13.5 로 중간값은 13.5가 된다.
이제 이를 직접 적용한 코드를 살펴본다.
코드

코드에 작은 부가 설명을 하자면, 함수의 첫번째 부분에서 nums1 길이가 nums2 길이보다 길면 매개변수를 서로 바꿔 다시 함수를 호출하도록 한다. 첫 번째 매개변수가 다른 배열보다 상대적으로 더 작은 배열이 되게끔 해야 풀이법이 적용되기 때문이다.
그리고 partitionX, partitionY 및 중간값을 구하는 부분에서 나누기를 하여 나오는 값이 정수값이 나오도록 해야되는 것에 유의하자.
출처
'Algorithm 개념 및 문제풀이 > Leetcode' 카테고리의 다른 글
| Leetcode 17번 문제 풀이 (0) | 2020.02.05 |
|---|---|
| Leetcode 15번 문제 풀이 (0) | 2020.02.03 |
| Leetcode 5번 문제 풀이 (0) | 2020.01.12 |
| Leetcode 3번 문제 풀이 (1) | 2020.01.09 |




댓글